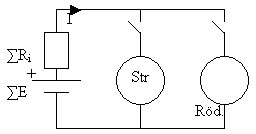
Lösning 4.2:5
FörberedandeFysik
Effekten \displaystyle P=U^2/R
Strålkastarlampans resistans är \displaystyle R_S=144/10=14,4\,\Omega,
rödljusets lampa \displaystyle R_R=144/5=28,8\,\Omega,
\displaystyle R_{S+R}=144/15=9,6\,\Omega
Kirchhoffs lag ger \displaystyle E-I\cdot R_I-I\cdot R=0
ger \displaystyle 8\cdot 1,65-I_S\cdot8\cdot0,1-I_S\cdot14,4=0 \Rightarrow I_S=0,87 \,\mathrm{A},
\displaystyle 8\cdot 1,65-I_R\cdot 8\cdot 0,1-I_R\cdot 28,8=0 \Rightarrow I_R=0,45 \,\mathrm{A},
\displaystyle 8\cdot 1,65-I_{R+S}\cdot 8\cdot 0,1-I_{R+S}\cdot 9,6=0 \Rightarrow I_{R+S}=1,27 \,\mathrm{A}
Kommentar:
Lite lurigt tal. Det är lätt att glömma bort att spänningen över lamporna sjunker då bägge lamporna är inkopplade.
Många som räknar på detta tal räknar som om spänningen för alla lampor var \displaystyle 12 \,\mathrm{V}\ oavsett belastningsfallet. Spänningsfallet över det inre motståndet ändras med strömmen som går genom motståndet. Det står stämplat på lamporna att det är en viss effekt vid \displaystyle 12 \,\mathrm{V}. Det betyder inte att det är \displaystyle 12 \,\mathrm{V} över lampan så fort den inkopplad i en godtycklig krets.