FörberedandeFysik

Teori

Övningar

FÖRFATTARE: Ian Cohen, KTH Mekanik

I den del av mekaniken som heter dynamik behandlas en kropp som en partikel, dvs en punkt som har massa men ingen utsträckning dvs ingen längd, ingen bredd, ingen höjd. En sådan idealiserad partikel kallas även för punktkropp.

Naturligtvis finns det i verkligheten inga punktkroppar. Tar man t.ex. en boll, skulle man bortse från bollens storlek och betrakta endast bollens läge vid en viss tidpunkt. Även bilar och andra ”stora” kroppar kommer att betraktas som partiklar. Därför skulle det här kapitlet lika bra kunna rubriceras som partikeldynamik.

För en mer exakt fysikalisk behandling där man även tar hänsyn till kropparnas utsträckning måste man studera en annan, mer avancerad del av mekaniken som heter stela kroppars mekanik.

Lägesbeskrivning

En partikel rör sig längs en känd bana. Det enklaste fallet är en rätlinjig bana. Man läser av partikelns läge vid varje tidpunkt \displaystyle t relativt till partikelns läge då \displaystyle t=0. Läget vid tiden \displaystyle t=0 kallas origo. Väljer man en riktning längs banan som positiv kan man beteckna läget eller positionen relativt till origo med \displaystyle s.

Rätlinjig bana:

Kroklinjig bana:

Ändringen av läget längs banan under en viss tid kallas tillryggalagd väg. Läget eller positionen \displaystyle s kan vara såväl positiv som negativ beroende på vilken sida om origo partikeln befinner sig. I fortsättningen kommer vi att behandla \displaystyle s som en slags koordinat vars värde är beroende av tiden. Rums- eller bankoordinaten \displaystyle s kan således anses som en funktion av tidskoordinaten \displaystyle t.

Medelhastighet

Tillryggalagd väg per tidsenhet, t.ex. \displaystyle 90 km/h , eller lite mer generellt tillryggalagd väg dividerad med tiden definieras som partikelns medelhastighet:

\displaystyle v=\frac{\text{tillryggalagd väg}}{\text{tidsintervall}}=\frac{\Delta s}{\Delta t}

där man mäter den tillryggalagda vägen \displaystyle \Delta s under ett visst tidsintervall \displaystyle \Delta t.

Symbolen \displaystyle \Delta används ofta inom de matematiska vetenskapliga områdena för att beteckna förändringen eller differensen (därav beteckningen med det grekiska delta).

Om hastigheten pekar i motsatt riktning mot \displaystyle s+ dvs om rörelsen går "bakåt", är hastigheten negativ.

Definitionen ovan är endast en approximation, närmare bestämt ett medelvärde därför att hastigheten kan vara varierande under det betraktade tidsintervallet. Men om hastigheten är konstant får man ett exakt svar för vilket tidsintervall som helst. Om hastigheten inte är konstant gäller följande: Ju mindre tidsintervall desto bättre approximation.

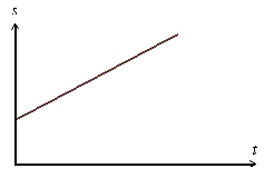
Man kan få en graf genom att rita förflyttningen \displaystyle s mot tiden \displaystyle t. Om hastigheten är konstant blir grafen en rät linje:

Momentanhastighet

Det är sällan man har konstant hastighet. Vid variabel hastighet ger den ovannämnda definitionen \displaystyle v=\frac{\Delta s}{\Delta t} endast medelhastigheten i hela tidsintervallet \displaystyle \Delta t=t_2-t_1. Momentanhastigheten vid en viss tidpunkt, ett ögonblick, får man inte fram med denna definition.

Om man tittar på hastighetsmätaren på en bil, ser man att hastigheten varierar. Om en bil åker cirka 70 km/h under större delen av en resa, men under en kort period åker 30 km/h pga vägarbete, kommer den att ha en medelhastighet på nästan 70 km/h för hela resan. Det visar att medelhastighet ofta säger väldigt litet om hastighet i ett visst ögonblick som t.ex. när bilen åker förbi vägarbetet. Så, vad menas egentligen med att bilen har hastigheten 50 km/h just nu?

Hastighet

För att få ett så bra mått som möjligt på hastigheten vid ett visst ögonblick \displaystyle t skall man låta tidsintervallet \displaystyle \Delta t=t_2-t_1 vara så litet som möjligt. Låter man intervallängden slutligen gå mot \displaystyle 0 övergår definitionen ovan till det som man kallar för ögonblicks- eller momentanhastighet. På vilket sätt övergången till tidsintervallängden \displaystyle 0 görs exakt, visas i matematikens disciplin envariabelanalys där momentanhastigheten definieras som
\displaystyle v=\frac{ds}{dt} dvs förflyttningens derivata med avseende på tiden.

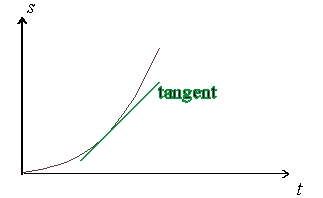
För att åskådliggöra hastighetens matematiska definition brukar man rita förflyttningen \displaystyle s mot tiden \displaystyle t. Grafen blir då inte längre är en rak linje (konstant hastighet) utan en böjd kurva (variabel hastighet). Då kan man läsa av hastigheten i grafens lutning. För att bestämma hastigheten från ett \displaystyle s-t diagram ritar man tangenten, dvs en rät linje som ”tangerar” grafen vid den tidpunkt \displaystyle t som man undersöker. Tangentens lutning anger hastigheten vid tidpunkten \displaystyle t:

I fortsättningen kommer vi att använda termen hastighet \displaystyle v för momentanhastighet.

Hastighet-tid-graf

Eftersom även hastigheten är beroende av tiden, är \displaystyle v en funktion av \displaystyle t och man kan rita hastighetsförloppet mot tiden. Då får man en hastighet-tid \displaystyle (v-t) graf. En viktig användning av ett \displaystyle v-t diagram är att arean under grafen anger förflyttningen \displaystyle s.

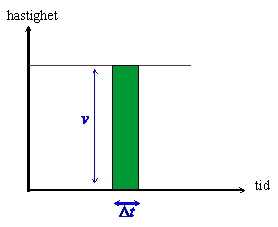
I specialfallet att hastigheten är konstant:

kan man lätt se detta eftersom

\displaystyle \Delta s = v\cdot \Delta t

Annars går det att bevisa med integrationsteori i envariabelanalys.

Acceleration

Hastighetsändringen dividerad med tiden definieras som partikelns medelacceleration:

\displaystyle a=\frac{\text{hastighetändring}}{\text{tidsintervall}}=\frac{\Delta v}{\Delta t}

där man mäter medelhastigheten \displaystyle \Delta v under ett visst tidsintervall \displaystyle \Delta t.

Medelacceleration brukar säga väldigt litet om accelerationen i ett visst ögonblick. På samma sätt som vid teorin om hastighet kan man använda envariabelanalys.
Man definierar matematiskt (momentan)accelerationen längs banan som \displaystyle a=\frac{dv}{dt}
dvs hastighetens derivata med avseende på tiden.

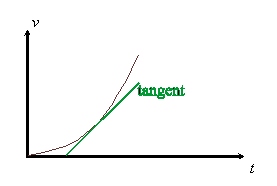
För att åskådliggöra accelerationens matematiska definition brukar man rita hastighet mot tid. I \displaystyle v-t grafen kan man läsa av accelerationen då den är kurvans lutning. För att bestämma accelerationen från ett \displaystyle v-t diagram ritar man tangenten, dvs en rät linje som ”tangerar” grafen vid tiden \displaystyle t som man undersöker:

Om accelerationen pekar i motsatt riktning mot \displaystyle s+ är accelerationen negativ.

I denna kurs kommer accelerationens storlek att alltid vara konstant och därmed medelaccelerationen lika med momentanaccelerationen.

Eftersom man har en positiv och negativ riktning hos banan, kan förflyttningen, hastigheten och accelerationen vara såväl positiva som negativa beroende på om de pekar i den positiva eller den negativa riktningen.

Förflyttningens storlek kallas avstånd, hastighetens storlek kallas fart. Det finns inget namn för accelerationens storlek.

Om accelerationen däremot har motsatt riktning mot hastigheten, kommer hastigheten att minska. Det motsvarar bromsning. Storleken hos denna omvända acceleration kallas retardation.

Formler vid likformigt accelererad rörelse

I denna kurs om dynamik behandlas endast fallet då accelerationen är konstant. (Om accelerationen är noll faller det under ämnet statik, se kursens del 2).

Gå igenom följande i tankarna:

1) Välj en lämplig tidpunkt där vi börjar mäta tiden, dvs bestäm tidpunkten \displaystyle t=0.

2) Börja mäta förflyttningen \displaystyle s från partikelns läge vid \displaystyle t=0. Det förenklar beräkningarna.

3) Låt partikeln ha en hastighet \displaystyle v_0 i början och en konstant acceleration \displaystyle a.

Då kan man visa följande.

\displaystyle v=v_0+a\cdot t

\displaystyle s=\frac{v_0+v}{2}\cdot t

\displaystyle s=v_0\cdot t+\frac{1}{2}\cdot a\cdot t^2

Ibland används följande som kan härledas från de andra ekvationerna:

\displaystyle v^2=v_{0}^{2}+2\cdot a\cdot s

Fritt fall

En partikel faller fritt nära jorden.

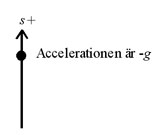
Om man bortser från luftmotståndet kommer den att ha en acceleration \displaystyle g mot jorden. Man brukar anta att \displaystyle g=9,82 m/s^2, men för många enklare uppgifter kan man göra beräkningarna smidigare genom att istället anta att \displaystyle g=10m/s^2. Om partikeln rör sig lodrätt, kan man välja ett lämpligt läge där \displaystyle t = 0 och mäta \displaystyle s uppåt från denna punkt. I så fall är accelerationen \displaystyle a = -g. Detta är ett typiskt exempel på en rätlinjig rörelse. Observera att hastigheten är negativ om partikeln rör sig neråt.

Man kan välja att mäta \displaystyle s neråt från origo, då gäller att \displaystyle a=g. Hur man gör är en smaksak.