FörberedandeFysik

Teori

Övningar

FÖRFATTARE: Christer Johannesson & Lars-Erik Berg, KTH Fysik

Elektriska kretsar

Elektrisk ström som definieras som laddningen passerar genom en tvärsnittsyta A för en ledning per tidsenhet. Strömmen är en skalär, men har riktning.

För att det i en elektrisk krets ska gå en kontinuerlig ström, måste kretsen innehålla ett element som fungerar som källa till elektrisk energi, en elektromotorisk kraft. Detta kan exempelvis vara ett batteri, en solcell eller en generator.

När ett batteri kopplas till ett motstånd, går en ström genom kretsen. Kopplas batteriet till en kondensator förflyttas laddningsbärare från den ena kondensatorskivan till den andra.

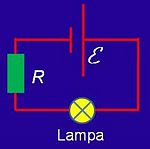
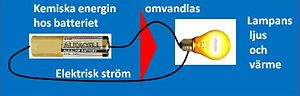
För att det skall kunna gå ström genom en strömkrets, måste kretsen vara sluten. I en strömkrets, som bildas av ett vanligt batteri och en glödlampa, syns elströmmens effekter i form av ljus och av att glödlampan värms upp.

Den kemiska energin från batteriet omvandlas till ljus och värme i strömkretsen som får lampan att lysa.

Genom att bygga olika slutna strömkretsar av batterier och lampor, kan man undersöka den elektriska strömmens egenskaper.

Batteriernas effekt förstärker varandra då de seriekopplas och de tar ut varandra då de kopplas mittemot varandra. Parallellkoppling inverkar inte på batteriernas styrkor.

Lampan glöder starkare ju fler batterier som kopplas till strömkretsen. Även de lampor som kopplas till batteriet inverkar ljusstyrkan. Lamporna glöder svagare då de är seriekopplade.

Ohms lag

Ström är transport av laddningar per tidsenhet, oftast elektroner, som kan ta sig fram i ledande material.

Det som bestämmer strömmens storlek är hur stort det elektriska fältet är och hur bra materialet är på att transportera laddningar. Det elektriska fältet kan vi få genom att ha en potentialskillnad eller spänning över materialet. Materialets resistans eller motstånd är ett mått på dess ledningsegenskaper.

Det uttryck som kopplar samman ström, spänning och resistans kallas Ohms lag.

\displaystyle U = I\cdot R

där
\displaystyle U är spänningen eller potentialskillnaden som mäts i volt, V
\displaystyle I är strömmen som mäts i ampere, A
\displaystyle R är motståndet eller resistansen som mäts i ohm, \displaystyle \Omega

I detta avsnitt används \displaystyle E för elektromotorisk spänning. \displaystyle E är i andra delar av kursen storheten för energi eller i andra avsnitt elektriska fält.

Strömmar och spänningar är adder- och subtraherbara. Detta leder till att man kan bilda nya ekvationer som bygger på att summan av alla spänningar runt i en krets är noll (Kirchhoffs spänningslag) och summan av alla strömmar in och ut ut en punkt i kretsen är noll (Kirchhoffs strömlag).

Ett par viktiga definitioner

Med polspänning menar vi spänningen mellan ett batteris eller en spänningskällas poler.

Strömmen i en krets definieras som att den går från plus- till minuspol. Numera vet man att elektronerna som utgör en elektrisk ström istället rör sig från minus- till pluspol.

Hur tänker man kring glödlampor och motstånd (resistorer)?

Motstånd (resistorer) är komponenter som leder ström men med motstånd. Motståndet gör att en del av den energi som förs igenom motståndet kommer att omvandlas till värme. I vissa fall är värme önskvärt som motståndstråden i en brödrost medan man inuti en bärbar dator helst vill ha så lite motstånd som möjligt för att slippa värme som måste ventileras ut och dessutom förbrukar batteri.

Komponenten motstånd består av ett material som leder ström dåligt och genom att anpassa dopning (materialsammansättning), tjocklek och längd kan man få fram komponenter med olika resistanser (mäts i ohm). Ett vanligt (eller idealt) motstånds resistans (mäts i ohm) ändras inte av olika frekvenser, temperaturer eller strömstyrkor.

En klassisk glödlampa består av en tunn tråd av metallen wolfram inuti en lufttät glaskula fylld med ädelgas för att bromsa upp förkolningen av wolframtråden. När det går en ström genom wolframtråden utstrålar den värmeförluster på sådan frekvenser som ögat uppfattar som synligt ljus. Lampan lyser. En glödlampa modelleras därför som en resistor när man räknar på dem. En glödlampa har en resistans men det som står stämplat på dem är ofta effekt och spänning. Från det går resistanen att räkna ut.

En ström som går genom ett motstånd ger upphov till ett spänningsfall över motståndet, vi använder Ohms lag för att beräkna detta spänningsfall enligt

\displaystyle U=R\cdot I

Exempel 1

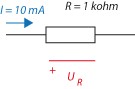
Genom ett motstånd på \displaystyle 1 \text{k}\Omega går det en ström på 10 mA. Hur stort blir spänningsfallet över motståndet?

Vi använder Ohms lag föra att beräkna spänningsfallet, får det till \displaystyle U=1\mathrm{k}\Omega \cdot 10\mathrm{mA}=10\mathrm{V}. Vi vet nu att spänningsfallet kommer att bli 10 V över detta motstånd om man skickar en ström på 10 mA genom det.

Exempel 2

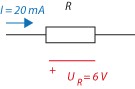
Vi vill ha en ström på 20 mA och ett spänningsfall på 6 V (vill vill driva en lysdiod som har ett spänningsfall på 3 V via ett niovoltsbatteri). Vilken resistans ska vi välja?

Vi utgår från Ohms lag \displaystyle U=R⋅I och omvandlar den med hjälp av algebra så att den blir på formen \displaystyle R=U/I. Med insatta värden får vi \displaystyle R=6\mathrm{V}/20\mathrm{mA}=300 \Omega.

Vi ska välja ett motstånd så nära 300Ω som möjligt (de tillverkas i standardvärden, 330Ω är närmast).

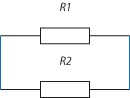
Seriekoppling av motstånd

Vad händer om man kopplar två motstånd efter varandra, hur stor blir då den totala resistansen?

Om vi tänker på vad ett motstånd är och att resistansen beror på dopning (materialsammansättning), tjocklek och längd och sedan funderar på vad som händer när vi sätter två motstånd efter varandra så kan man ju lätt tänka att längden blir längre medan tjocklek och material knappast påverkas förutsatt då att det är samma typ av motstånd. Den totala resistansen och därmed spänningsfallet borde bli högre (omöjligen mindre). Det matematiska sambandet lyder för två seriekopplade motstånd med respektive värde \displaystyle R_1 och \displaystyle R_2 att den totala resistansen fås enligt sambandet

\displaystyle R_{tot}=R_1+R_2

Mer allmänt gäller för j seriekopplade resistorer

\displaystyle R_{tot}=\sum_j R_j

Exempel 3

Vi seriekopplar två motstånd med värdena 3,9Ω och 4,3Ω och söker den totala resistansen.

Från sambandet för seriekoppling av motstånd med insatta värden har vi \displaystyle R_{tot}=R_1+R_2=3,9\Omega+4,3\Omega=8,2\Omega.

Den totala resistansen (eller om man så vill ersättningsresistansen) för dessa två motstånd är 8,2Ω.

Parallellkoppling av motstånd

Om man parallellkopplar flera motstånd får strömmen en ’bredare’ väg att ta sig fram genom motståndet och det förväntade spänningfallet över motståndet borde därför vara lägre än över motstånden var för sig. Eftersom strömmen får en ’bredare’ väg genom motståndet är de förväntade förlusterna och värmeutvecklingen också lägre.

Det matematiska sambandet lyder för två parallellkopplade motstånd med respektive värde \displaystyle R_1 och \displaystyle R_2 att den totala resistansen fås enligt sambandet

\displaystyle \frac{1}{R_{tot}} = \frac{1}{R_1} + \frac{1}{R_2}

Detta kan vi skriva om (med hjälp av algebra, prova gärna själv) till

\displaystyle R_{tot} = \frac{R_1\cdot R_2}{R_1 + R_2}

Allmänt gäller för j parallellkopplade resistorer att

\displaystyle \frac{1}{R_{tot}} = \sum_j \frac{1}{R_j}

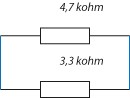
Exempel 4

Vi parallellkopplar två motstånd med värdena 4,7kΩ och 3,3kΩ, vilken blir den totala resistansen?

Från sambandet för parallellkopplade motstånd har vi att den totala resistansen (eller om man så vill ersättningsresistansen) blir

\displaystyle R_{tot} = \frac{4,7\cdot 3,3}{4,7 + 3,3} k\Omega \approx 1,9 k\Omega

Motståndsnät med fler än två motstånd

Ibland behöver man räkna på större nät med fler än två motstånd och söker kanske den totala resistansen. Då brukar en klok strategi vara att börja klumpa ihop dom två och två och räkna. Kanske hittar du två som sitter i serie, räkna då ut dessa tvås ersättningsresistans och skriv in den (exakt utan avrundning) i ett omritat kopplingsschema. Hitta några andra som kanske sitter parallellt och räkna ihop dem med formeln ovan. Rita om kopplingsschemat igen med denna komponent och håll på så tills bara en enda resistor återstår.

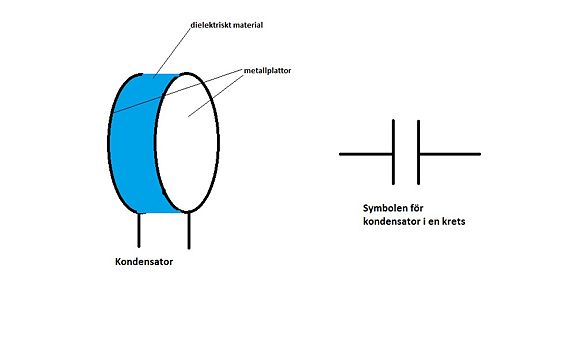
Kondensatorer

Kondensatorer är komponenter som har förmågan att lagra elektrisk laddning och därmed energi, ungefär som ett batteri. Kondensatorer används till exempel i radioapparater: när man byter radiostation genom att vrida på en ratt så ändrar man kondensatorns kapacitans. Kondensatorer kan också användas till att stabilisera spänningen i kretsen.

En kondensator består av två metallplattor som sitter parallellt mot varandra, med ett litet avstånd mellan dem. Materialet mellan plattorna kallas för dielektriskt material. Dielektriska material är material som inte leder ström. Det går ingen ström mellan plattorna i kondensatorn när den är helt uppladdad/urladdad.

När man ansluter ett batteri till en krets med en kondensator i så laddas plattorna i kondensatorn upp. En spänning byggs upp mellan plattorna när de laddas. Det innebär att elektroner ”hoppar” från ena plattan till den andra. Under denna tid så flyter ström igenom kondensatorn. Kondensatorn fortsätter att laddas tills spänningen mellan plattorna är lika stor som batteriets spänning. När kondensatorn har laddats klart, så förflyttas inga elektroner längre mellan plattorna, d.v.s. det går ingen ström längre genom kondensatorn.

Kondensatorns laddning är proportionell mot spänningen.

\displaystyle Q=C\cdot U

där \displaystyle Q är den elektriska laddningen, som mäts i coulomb, C

\displaystyle C är proportionalitetskonstanten, och kallas för kapacitans (mäts i farad). Kapacitans är alltså ett mått på kondensatorns förmåga att lagra elektrisk laddning.

\displaystyle U är spänningen eller potentialskillnaden.

Kondensatorns energi kan skrivas som

\displaystyle E = \frac{1}{2} U\cdot Q = \frac{1}{2}D\cdot U^2

där \displaystyle E är den lagrade energin, som mäts i joule, J.

Något om batterier och andra spänningskällor

Inom elläran behöver man komponenter som höjer spänningen i en krets. Ett batteri eller en inkopplad transformator är typiska komponenter som kan öka en potential i en krets.

Symbolen för ett batteri är två parallella tvärställda streck där den positiva polen har det längre strecket.

Då batteriet belastas genom någon yttre krets blir spänningen över polerna (polspänningen) den elektromotoriska spänningen minus strömmen från batteriet multiplicerad med batteriets inre resistans. Hos ficklampsbatterier och batterier till mobil utrustning brukar inre motståndet vara runt 1 Ω. För startbatterier till bilar, elektriska truckar, rullstolar mm brukar den inre resistansen eller inre motståndet, som man ofta säger, vara 1-10 mΩ.

Laddningsbara batterier kan laddas genom att ström förs till batteriet. Den yttre spänningskällan måste då ha en högre spänning än den elektromotoriska spänningen. Den pålagda spänningen måste vara den elektromotoriska spänningen plus strömmen multiplicerad med batteriets inre resistans för att uppladdning ska kunna ske.

Kirchoffs strömlag (kallas även K1 eller KCL)

Summan av alla strömmar från och till en punkt är alltid noll. Detta gäller för elektrisk ström men även för vätskor och gaser och andra partikelströmmar. Tänk dig t.ex. en å som ett dike rinner ut i. Vattenmängden efter det att diket runnit ut i ån är då vad som fanns i ån innan plus det som tillfördes via diket. Kirchoffs strömlag gäller bara elektrisk ström men sambandet han beskriver gäller mer allmänt.

Antag att vi har en elektrisk krets med en punkt där ett antal trådar går ihop. Vi kan då om vi vet alla strömmar utom en i denna punkt med hjälp av Kirchoffs strömlag bestämma den sista.

Matematiskt brukar vi skriva

\displaystyle I_1+I_2+...+I_n = 0

Eller om man så vill

\displaystyle \sum_n I_n=0

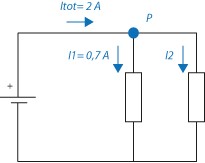
Exempel 5

Strömmen 2 A går från ett batteri vidare genom två parallellkopplade motstånd. Man vet att strömmen genom det första motståndet är 0,7 A och söker strömmen genom det andra motståndet.

Vi vet att strömmen 2 A går in i punkten P medan en av strömmarna som går ut ur punkten P är 0,7 A . Eftersom summan av alla strömmar i en punkt alltid är noll enligt Kirchoffs strömlag så kan vi teckna sambandet \displaystyle I_{tot}+I_1+I_2=0 där \displaystyle I_2 är den okända sökta strömmen.

Med hjälp av algebra omformar vi så att vi får \displaystyle I_2=I_{tot}−I_1=2\mathrm{A} −0,7\mathrm{A}=1,3\mathrm{A}.

Genom det andra motståndet går strömmen 1,3 A.

Slutna och öppna kretsar

En krets är en samling komponenter som sitter ihop på något sätt, exempelvis kan ett batteri sitta ihop med en lampa och en strömbrytare så att lampan lyser när man trycker på strömbrytaren och är släckt annars.

En krets är sluten när den sitter ihop, i fallet ovan sitter kretsen ihop när strömbrytaren är på.

En öppen krets har ett avbrott någonstans varför det inte kan gå några strömmar genom den.

Kirchoffs spänningslag (kallas även K2 eller KVL)

Summan av samtliga spänningsförändringar i en sluten krets är alltid noll.

\displaystyle \sum u_i = 0

Där \displaystyle u_i är spänningsförändringar över respektive komponent i den slutna kretsen.

Exempel 6

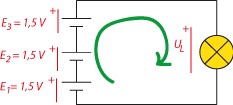
Tre 1,5 V-batterier är seriekopplade och till dem är en lampa ansluten och permanent inkopplad så att den lyser. Hur stor blir spänningen över lampan?

Vi börjar med att rita en pil (grön) i den slutna kretsen för att markera i vilken riktning vi rör oss. En spänningskälla (batteri) i denna riktning innebär att spänningen ökar och en passiv komponent (lampa, resistor) innebär att spänningen minskar. Summan av alla spänningar blir alltid enligt Kirchoffs spänningslag noll vilket vi kan utnyttja för att beräkna det sökta \displaystyle U_L.

I kopplingsschemat har vi satt ut värdena \displaystyle E_1, \displaystyle E_2 och \displaystyle E_3 över batterierna och \displaystyle U_L över lampan. Vilken ända av respektive komponent som har den högsta potentialen markeras med ett ’+’-tecken i illustrationen.

Kirchoffs spänningslag ger nu att \displaystyle E_1+E_2+E_3+U_L=0

Sätter vi in kända värden får vi \displaystyle 1,5\mathrm{V}+1,5\mathrm{V}+1,5\mathrm{V}+U_L=0, omskrivning med hjälp av algebra ger

\displaystyle U_L=−4,5V

Spänningsfallet över lampan blir alltså enligt Kirchoffs lag 4,5 V.

Ideala och verkliga komponenter

En ideal komponent är en komponent som beter sig precis som formeln säger och inte har några oönskade andra egenskaper. Sådana komponenter finns inte i verkligheten.

Om en ström tas ut ur ett batteri kommer det att uppstå värme i batteriet eftersom materialet som battericellerna är gjorda av har en viss resistans. En modell för ett verkligt batteri är därför ett idealt batteri seriekopplat med ett (litet) motstånd som motsvarar förlusterna i batteriet. Modellen kan bli krångligare än så om man tar hänsyn till de kemiska förändringarna som inträffar i batteriet beroende på hur stor laddning det har men detta ovan är en ofta använd modell.

Om ett batteri är obelastat går ingen ström genom batteriets inre motstånd och det är den elektromotoriska spänningen som kan mätas eller registreras.

Exempel 7

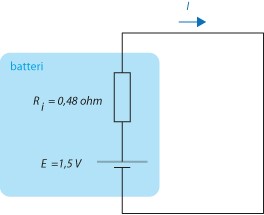
Ett vanligt ficklampsbatteri modell ’R20’ har en spänning obelastat på 1,5 V och en inre resistans på 0,48Ω. Hur stor skulle strömmen bli om man kortslut ’+’ och ’-’ på detta batteri?

Om ficklampsbatteriet hade varit 'idealt' så hade en oändligt stor ström gått mellan polerna men så kommer inte att ske eftersom ficklampsbatteriet är en verklig komponent som också har andra icke önskvärda egenskaper.

Vi ritar upp ett kopplingsschema över den slutna kretsen (när batteriet är kortslutet)

Från kopplingsschemat inser vi att spänningsfallet över den inre resistansen när batteriet är kortslutet måste vara lika stort som batteriets spänning. Med denna insikt kan vi använda Ohms lag \displaystyle U=R\cdot I för att beräkna kortslutningsströmmen till

\displaystyle I=\frac{U}{R}=\frac{1,5}{0,48}\mathrm{A} \approx 3,1\mathrm{A}

Denna ström är den största möjliga ström som går att få ut ur denna batterisort men sannolikt går en så stor ström bara att få ut under en kort tid innan batteriet har laddats ur.