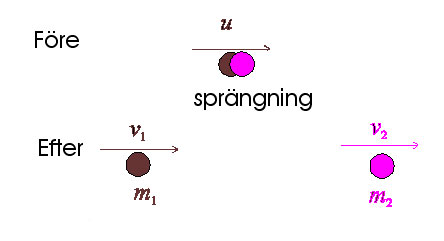FörberedandeFysik

Teori

Övningar

FÖRFATTARE: Ian Cohen, KTH Mekanik

Rörelsemängd

I förra avsnitt multiplicerade vi en partikels förflyttning med den kraft som verkade på den för att få partikelns arbete och energi.

Vad händer om man multiplicerar kraften som verkar på en partikel med den tid den verkar? Det blir \displaystyle Ft och leder oss till en ny fysikalisk storhet: Rörelsemängd.

Med hjälp av Newtons andra lag \displaystyle F=ma och andra kända formler kan vi uttrycka rörelsemängden på ett lite mer begripligt sätt:

Först följer av det ovan sagda \displaystyle Ft =mat.

Sedan kan vi skriva om \displaystyle v=v_0+at (se avsnitt 3.1 Liljebunden rörelse, Formler vid likformigt accelererad rörelse) till \displaystyle at=v-v_0 så att vi får:

\displaystyle Ft=m(v-v_0)=mv-mv_0

där \displaystyle mv kallas partikelns rörelsemängd och betecknas med \displaystyle p. Således har en partikel med massa \displaystyle m och hastigheten \displaystyle v rörelsemängden \displaystyle p=mv. Man kan säga att kraften \displaystyle F har ändrat partikelns rörelsemängd.

Rörelsemängden har en enhet som är produkten av enheterna för massa och hastighet, nämligen 1 kg m/s.

Rörelsemängd och energi hos en kropp är två helt skilda kinetiska storheter och beskriver olika fysikaliska egenskaper. Även matematiskt skiljer de sig:

Medan energi är en skalär är rörelsemängden en vektor och har därmed även en riktning. När det t.ex. gäller rörelse längs en rät linje kan hastigheten vara såväl positiv som negativ, varför även rörelsemängden kan vara såväl positiv som negativ.

Impulslagen vid rätlinjig rörelse

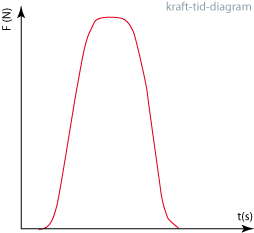
Om en kropp utsätts för en (relativt) stor kraft under en (relativt) kort tid, kan det vara svårt att ange kraftens styrka. Den brukar ha en mycket varierande styrka under den korta tid den verkar. Vid sådana situationer kan ett typiskt kraft-tid diagram se ut så här (den vertikala axeln visar kraften F och tiden mäts i sekunder):

För att få ett grepp om kraftens inverkan mäter vi ändringen i kroppens rörelsemängd. Med hjälp av envariabelanalys kan man visa att ändringen i rörelsemängden är lika stor som arean under kurvan. Denna ändring kallas kraftens impuls \displaystyle I.

Impuls = ändring i rörelsemängden eller \displaystyle I=\Delta p.

Vi bortser här från storheternas vektoregenskap (riktning) och tittar endast på deras storlek.

Vi kan få en uppskattning av den inblandade kraftens storlek om vi delar impulsen med tiden:

\displaystyle F_{medel}=\frac{impuls}{tid}

Exempel:

En ishockeypuck har en fart på \displaystyle 12 \text{m/s} då den träffas av klubban som ger den samma fart i motsatt riktning. Pucken har massan \displaystyle 0,2 \text{kg}. Slaget tar \displaystyle 0,04 \text{s}.

Ändringen i rörelsemängden = (ändringen i hastighet) (massa) = \displaystyle (24\text{m/s})(0,2\text{kg})=4,8\text{kgm/s} Det betyder att impulsen är \displaystyle I=4,8\text{ kgm/s}.

\displaystyle F_{medel}=\frac{4,8\text{kg m/s}}{0,04\text{s}}=120 \text{N} som ger en uppfattning av krafterna i ishockey.

Rörelse vid rak stöt, Newtons tredje lag och rörelsemängdens bevarande

Om två kroppar kolliderar kan vi anta att krafterna är (relativt) stora och att själva kollisionen sker under en (relativt) kort tid. Vi kallar denna händelse för en stöt.

I sådana situationer utsätts båda kroppar för en impuls. Enligt Newtons tredje lag måste impulsen på den ena kroppen vara motsatsen till impulsen på den andra. Eftersom impuls ändrar rörelsemängd, måste ändringen i den ena kroppens rörelsemängd vara motsatsen till ändringen i den andras rörelsemängd.

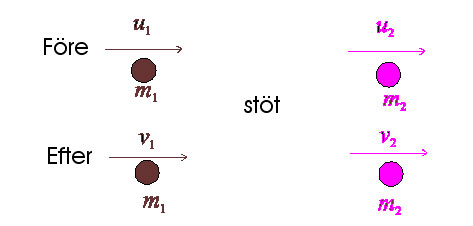
Vi kan dra slutsatsen att kropparnas totala rörelsemängd är densamma före och efter stöten:

Principen är känd under rörelsemängdens bevarande och kan skrivas som:

\displaystyle m_1u_1+m_2u_2=m_1v_1+m_2v_2

Lagen om rörelsemängdens bevarande gäller även om fler än två kroppar är inblandade.

Med samma resonemang kan vi konstatera att om en kropp plötsligt delar upp sig i bitar, måste rörelsemängden hos den ursprungliga kroppen vara lika stor som den totala rörelsemängden efteråt, vilket också kan betraktas som en stöt:

Nu får rörelsemängdens bevarande följande form:

\displaystyle (m_1+m_2)u=m_1v_1+m_2v_2

Det är viktigt att påpeka att slutsatsen att rörelsemängden är konstant, gäller precis före och efter stöten.

Under en längre tid efter stöten kan friktion påverka rörelsemängden.

Elastisk och oelastisk stöt

Två specialfall av stöt tas upp.

1) Vi antar att förlusten av kinetisk energi är obetydlig och gör approximationen att den kinetiska energin är samma före som efter stöten. En sådan stöt kallas elastisk.

Då har vi:

\displaystyle \frac{1}{2}m_1u_1^2+\frac{1}{2}m_2u_2^2=\frac{1}{2}m_1v_1^2+\frac{1}{2}m_2v_2^2

Vid alla stötförlopp gäller:

\displaystyle m_1u_1+m_2u_2=m_1v_1+m_2v_2

2) Om kropparna fastnar efter stöten förloras kinetisk energi. Man kan visa att denna sorts stöt leder till maximal förlust av kinetisk energi. En sådan stöt kallas oelastisk. Då får vi:

\displaystyle m_1u_1+m_2u_2=(m_1+m_2)v

Vid en sprängning ökar den kinetiska energin, dvs den kinetiska energin är inte densamma före och efter.

Observera att hastighet och rörelsemängd är vektorer. I figurerna ovan har vi den positiva riktningen till höger. Om kroppen har en hastighet till vänster måste vi ha ett minustecken framför farten. T.ex.:

Anmärkning: Vi har i detta avsnitt endast behandlat rätlinjig rörelse.