FörberedandeFysik

Teori

Övningar

FÖRFATTARE: Göran Karlsson, KTH Mekanik

Krafter

Kraft är ett viktigt begrepp i fysiken. En kraft representeras av en vektor som tillordnats en angreppspunkt.

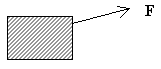
Man bör försöka rita vektorns fotpunkt i angreppspunkten. Låt oss ta exemplet med en låda som man drar med hjälp av ett lätt rep. Därvid frilägger man lådan dvs tar bort repet och placerar vektorns fotpunkt i den punkt där repet satt – angreppspunkten:

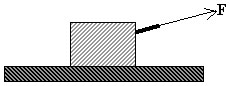
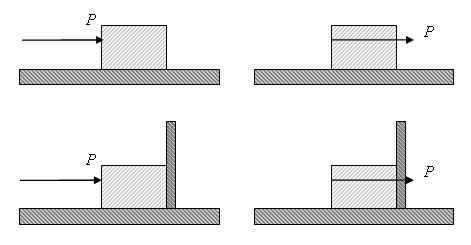
Ibland, när man t.ex. trycker på en kropp, kan det vara tydligare att placera vektorns spets i angreppspunkten (som i vänstra figuren nedan). Man kan dock i stället även då välja att placeras vektorns fotpunkt i angreppspunkten (som i högra figuren nedan). Det blir samma verkan, vilket visar att man kan förflytta vektorer längs deras verkningslinjer utan att det blir någon skillnad.

De figurer som ritats ovan är naturligtvis inte fullständiga. Dels saknas omgivningarna (underlaget, personen som trycker, väggar etc) och dels saknas övriga krafter.

Låt oss titta hur dessa figurer skulle se ut om omgivningarna togs med.

I den första figuren har vi enbart lådan som släpas via repet över golvet:

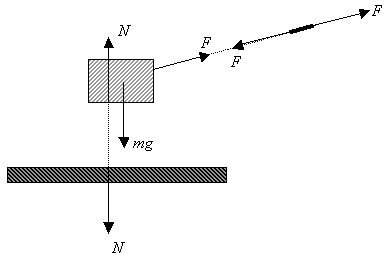
Men låt oss nu frilägga lådan. Detta innebär att vi isolerar den från alla andra kroppar den är i kontakt med. Detta gör vi för att kunna markera de krafter som verkar på lådan (direkt eller indirekt genom en annan kropp). Vi har även frilagt tråden, som då placeras på avstånd från lådan, så långt bort att vi får plats att rita krafter på såväl lådan som tråden. Vi sätter ut samtliga krafter som verkar på lådan respektive tråden:

Observera några punkter:

1) Kraftpilarna har ritats något annorlunda, så här:

i stället för:

och dessutom har fet symbol för kraften F bytts mot komponentbeteckning \displaystyle F. Orsaken till detta är följande: Om man inte speciellt behöver framhäva vektoregenskapen, är det mer praktiskt att tänka sig att den är den symbol som man sätter ut vid pilen för att representera komponenten av vektorn (dvs kraften) i pilens riktning. Gör man så får man inga problem med tecken för kontaktkrafter enligt Newtons tredje lag, eftersom samma beteckningar kan användas. Sedan vid beräkningar får man positiva komponenter t ex uppåt och negativa komponenter nedåt.

2) Genom att vi har repet som drar snett uppåt slipper vi ett rittekniskt problem som skulle ha uppstått om inget rep funnits: Då skulle normalkraftens pil hamnat rakt över tyngdkraftens pil, om kraften F varit horisontell.

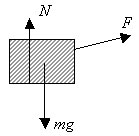
3) Den kraft som verkar från golvets underlag har inte ritats ut, eftersom vi inte vet hur golvet är upphängt. När man gör beräkningar ska alla krafter tas med för alla de kroppar man räknar på. Eftersom repet är lätt är det endast lådan man behöver betrakta:

Låt oss nu titta på hur man frilägger en låda som man trycker på om det finns en vägg eller inte:

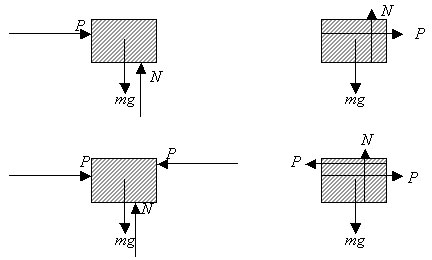
Friläggning:

I största möjliga utsträckning bör det högra sättet att rita användas. Observera att de om ingen vägg finnes (övre figurerna), så kan lådan inte vara i jämvikt (om friktion saknas).

Gravitationskraften

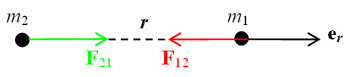
På partikel 1 från partikel 2 är \displaystyle \displaystyle \,\,\,\, \mathbf{F}_{12} = - G \frac{m_1m_2}{r^2}\mathbf{e}_r , där universella gravitationskonstanten \displaystyle G = 6,67 \cdot 10^{-11}\,\textrm{ m}^3\textrm{kg}^{-1}\textrm{s}^{-2}.

Enligt Newtons tredje lag är gravittionskraften på partikel 2 från partikel 1: \displaystyle \displaystyle \mathbf{F}_{21} = G \frac{m_1m_2}{r^2}\mathbf{e}_r

Tyngdkraften

approximerar väl gravitationskraften på jordytan om tyngdaccelerationen \displaystyle \displaystyle \mathbf{g} = -G \frac{m_2}{R^2} \mathbf{e}_y, där \displaystyle R är jordens radie och där \displaystyle y-axeln valts rakt uppåt. Dessutom har y-axeln konstant riktning, varför den är vinkelrät mot horisontalplanet, vilket är tangentplan till jordytan och som således inte följer jordytans krökning. \displaystyle g varierar på jordytan, men på vår latitud är \displaystyle g = 9,80665\, \textrm{m/s}^2. För våra problem brukar vi dock använda \displaystyle g = 9,82\,\textrm{m/s}^2.

Elektromagnetiska krafter

kan beskrivas med formeln \displaystyle \displaystyle \mathbf{F} = Q_1(\mathbf{E}+\mathbf{v}\times\mathbf{B}) , där \displaystyle Q_1 är partikelns laddning, \displaystyle \mathbf{v} dess hastighet. \displaystyle \mathbf{E} är den elektriska fältstyrkan och \displaystyle \mathbf{B} den magnetiska flödestäthen.

Den elektriska fältstyrkan kring en partikel med laddningen \displaystyle Q_2 i vakuum är \displaystyle \displaystyle \mathbf{E} = \frac{1}{4\pi\varepsilon_0}\frac{Q_2}{r^2}\mathbf{e}_r , där dielektricitetskonstanten i vakuum är \displaystyle \varepsilon_0 = 8,8544 \cdot 10^{-12}\textrm{N}^{-1}\textrm{m}^{-2}\textrm{A}^2\textrm{s}^2.

Coulombs lag

Den elektrostatiska kraften på partikel 1 från partikel 2 är \displaystyle \displaystyle \mathbf{F}_{12} = \frac{1}{4\pi\varepsilon_0}\frac{Q_1Q_2}{r^2}\mathbf{e}_r .

Andra exempel på krafter:

1) Stark och svag växelverkan; kärnkrafter.

2) Kontaktkrafter mellan kroppar:

Friktionskraft och normalkraft.

3) Elastiska krafter:

För en fjäder eller elastisk tråd är kraften som behövs för att dra ut fjädern eller tråden en sträcka \displaystyle \mathbf{F} = k\,x\,\mathbf{e}_x . Den återförande kraft som verkar på en partikel i fjäderns ändpunkt är då enligt Newtons tredje lag \displaystyle -\mathbf{F} = -\,k\,x\,\mathbf{e}_x

4) Viskösa krafter:

Kraften på en kropp som rör sig med hastigheten \displaystyle \mathbf{v} = v\,\mathbf{e}_x i en stillastående vätska är \displaystyle \mathbf{F} = -\,d\,v\,\mathbf{e}_x

5) Trådkrafter:

Kraften i en fri, lätt, böjlig tråd är riktad längs tangenten. Trådar kan endast ta upp dragkrafter och inte tryckkrafter.