Kylmaskiner och värmepumpar
FörberedandeFysik
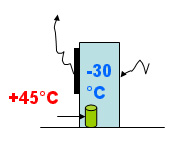
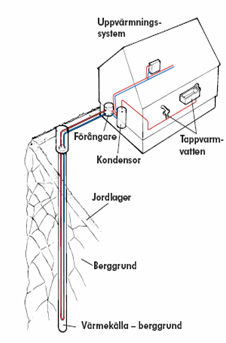
En kylprocess i ett kylskåp tar värme från den kalla maten och luften inne i själva skåpet och avger värme genom de svarta slingorna på baksidan. På samma sätt kan en värmepump ta värme från kall jord eller berggrund och avge värme inne i ett varmt hus. Vanligtvis drivs kylskåp och värmepumpar av el. Clausius formulering av den andra huvudsatsen hävdar att de måste drivas för att kunna åstadkomma värmeöverföring åt fel håll, från kallt till varmt.
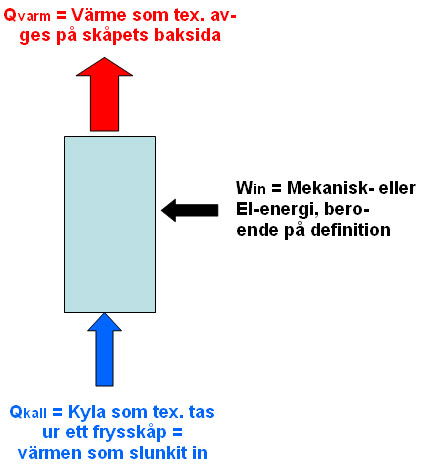
Den första huvudsatsen leder till en energibudget för kylprocesser och värmepumpar som kan uttryckas så här:
\displaystyle Q_{\rm varm} \;=\; Q_{\rm kall} \;+\; W_{\rm in}
där \displaystyle \:Q_{\rm varm}\: är värme överfört från maskinen på den varma sidan. \displaystyle Q_{\rm kall}\: är värme överfört till maskinen på den kalla sidan, och \displaystyle \:W_{\rm in}\: är mekanisk energi fört till maskinen, t.ex. el.
Alla 'prestationstal', så kallade godhetstal, har samma generell struktur: Det är kvoten mellan 'vad man vill ha' och 'vad det kostar'.
För en kylprocess som t.ex. ett kylskåp, motsvaras "vad man vill ha" av det värmet \displaystyle \:Q_{\rm kall}\: som förs från den kalla sidan medan "vad det kostar" är det arbetet \displaystyle \:W_{\rm in}\: som tillförs som el. Det relevanta prestationstalet är köldfaktorn \displaystyle \:COP_{\rm kyl}\: som är kvoten mellan \displaystyle \:Q_{\rm kall}\: och \displaystyle \:W_{\rm in}:
\displaystyle COP_{\rm kyl} = \displaystyle \frac {Q_{\rm kall}}{W_{\rm in}}
"COP" står för den engelska frasen "Coefficient of performance" (prestationstal).
Jämför verkningsgraden för en motor
Den andra huvudsatsen visar att köldfaktorn för ett kylskåp inte kan vara större än kvoten mellan den kalla temperaturen, \displaystyle T_{\rm min}, och temperaturskillnaden \displaystyle T_{\rm max}-T_{\rm min},
\displaystyle COP_{\rm kyl} \quad \le \quad \displaystyle \frac{T_{\rm min}}{T_{\rm max}-T_{\rm min}}
Det är viktigt att temperaturerna i detta uttryck ligger på en temperaturskala med rätt nollpunkt, till exempel Kelvinskalan.
För en värmepump motsvaras 'vad man vill ha' av det värmet \displaystyle \:Q_{\rm varm}\: som förs till den varma sidan medan 'vad det kostar' är det arbetet \displaystyle \:W_{\rm in}\: som tillförs som el. Det relevanta prestationstalet är värmefaktorn \displaystyle \:COP_{\rm vp}\: som är kvoten mellan \displaystyle \:Q_{\rm varm}\: och \displaystyle \:W_{\rm in}\::
\displaystyle COP_{\rm vp} = \displaystyle \frac{Q_{\rm varm}}{W_{\rm in}}
Den andra huvudsatsen visar att värmefaktorn för en värmepump inte kan vara större än kvoten mellan den varma temperaturen \displaystyle \: T_{\rm max}\: och temperaturskillnaden \displaystyle T_{\rm max} - T_{\rm min}
\displaystyle COP_{\rm vp} \quad \le \quad \displaystyle\frac{T_{\rm max}}{T_{\rm max }-T_{\rm min}}
Det är viktigt att temperaturerna i detta uttryck ligger på en temperaturskala med rätt nollpunkt, t. ex. Kelvinskalan.