Exempel uppgift
FörberedandeFysik
| (20 mellanliggande versioner visas inte.) | |||
| Rad 31: | Rad 31: | ||
<b>E3</b>. En plastlinjal är drygt 20 cm lång. Vid markeringen för 10 cm finns ett hål i linjalen i vilket man kan sticka in t.ex. en stoppnål. Denna fungerar då som en axel kring vilken linjalen blir vridbar. En metallstav <math>S</math> och en motvikt <math>M</math> håller varandra i jämvikt, när de är placerade som i figuren. Båda hänger i mycket tunna trådar. Metallstavens volym är 10,0 cm<math>^3</math>. | <b>E3</b>. En plastlinjal är drygt 20 cm lång. Vid markeringen för 10 cm finns ett hål i linjalen i vilket man kan sticka in t.ex. en stoppnål. Denna fungerar då som en axel kring vilken linjalen blir vridbar. En metallstav <math>S</math> och en motvikt <math>M</math> håller varandra i jämvikt, när de är placerade som i figuren. Båda hänger i mycket tunna trådar. Metallstavens volym är 10,0 cm<math>^3</math>. | ||
| + | |||
| + | [[Bild:Sh112n_e3_fig1.JPG]] | ||
En bägare med vätska placeras så att metallstaven i sin helhet blir omgiven av vätskan. För att återställa jämvikten hänger man vid lämpliga skalstreck (se figuren nedan) små ståltrådar med massorna 0,1 g, 1 g och 10 g. | En bägare med vätska placeras så att metallstaven i sin helhet blir omgiven av vätskan. För att återställa jämvikten hänger man vid lämpliga skalstreck (se figuren nedan) små ståltrådar med massorna 0,1 g, 1 g och 10 g. | ||
| + | |||
| + | [[Bild:Sh112n_e3_fig2.JPG]] | ||
Bestäm vätskans densitet om, som i figuren, ståltrådarna måste hängas på avstånden 3 cm, 7 cm respektive 8 cm från vridningsaxeln. | Bestäm vätskans densitet om, som i figuren, ståltrådarna måste hängas på avstånden 3 cm, 7 cm respektive 8 cm från vridningsaxeln. | ||
| Rad 97: | Rad 101: | ||
<math>240 \left( \cos{32}\cdot \tan{48} - \sin{32} \right) = c\left( \cos{72}\cdot \tan{48} + \sin{72} \right)</math> | <math>240 \left( \cos{32}\cdot \tan{48} - \sin{32} \right) = c\left( \cos{72}\cdot \tan{48} + \sin{72} \right)</math> | ||
| - | <math>\Rightarrow c = 240 \cdot \displaystyle\frac{\cos{32}\cdot \tan{48} - \sin{23}}{\cos{72}\cdot\tan{48}+ \sin{72}} \approx | + | <math>\Rightarrow c = 240 \cdot \displaystyle\frac{\cos{32}\cdot \tan{48} - \sin{23}}{\cos{72}\cdot\tan{48}+ \sin{72}} \approx 76 </math> |
Det exakta värdet av <i>c</i> insatt i (1) överst ger b enligt | Det exakta värdet av <i>c</i> insatt i (1) överst ger b enligt | ||
| Rad 103: | Rad 107: | ||
<math> 240 \cdot \cos{32} - 240 \cdot \cos{72} \displaystyle\frac{\cos{32}\cdot\tan{48}-\sin{32}}{\cos{72} \cdot \tan{48} + \sin{72}}</math> | <math> 240 \cdot \cos{32} - 240 \cdot \cos{72} \displaystyle\frac{\cos{32}\cdot\tan{48}-\sin{32}}{\cos{72} \cdot \tan{48} + \sin{72}}</math> | ||
| - | <math>\Rightarrow b = \displaystyle\frac{240}{\cos{48}} \cdot \left( \cos{32} - \cos{72} \displaystyle\frac{\cos{32}\cdot\tan{48}-\sin{32}}{\cos{72} \cdot \tan{48} + \sin{72}} \right) \approx | + | <math>\Rightarrow b = \displaystyle\frac{240}{\cos{48}} \cdot \left( \cos{32} - \cos{72} \displaystyle\frac{\cos{32}\cdot\tan{48}-\sin{32}}{\cos{72} \cdot \tan{48} + \sin{72}} \right) \approx 269 </math> |
====E3==== | ====E3==== | ||
| + | Vi antar att det snöre som den stora metallstaven hänger i har massan noll och är styvt. Det innebär att det inte påverkar jämviktsekvationen och att en eventuell kraft riktad uppåt på metallstaven kommer att innebära att linjalen rör sig uppåt. Med detta antagande kan problemet lösas. | ||
| + | |||
| + | Vid en första anblick ser det ut som att vi ska sätta upp en jämviktsekvation för de två fallen och utifrån det plocka fram de obekanta massorna. Man inser ganska snart att detta inte hjälper, vi får fler obekanta än antalet ekvationer. Vi har inte heller så stor nytta av att få reda på de absoluta massorna för M och S i figuren. | ||
| + | |||
| + | Den huvudsakliga skillnaden mellan de båda fallen är att metallstaven i det senare är nedsänkt i en vätska. Vi misstänker att Archimedes princip kan vara användbar och drar oss den till minnes: | ||
| + | |||
| + | Archimedes princip<br/> | ||
| + | <i>Lyftkraften på ett föremål i en vätska är lika stor som tyngden av den undanträngda vätskan.</i> | ||
| + | |||
| + | Om vi sätter upp en jämviktsekvation kring knappnålen för skillnaden mellan fall 1 och fall 2 bör vi kunna få ut lyftkraften <math>F_L</math> som uppstår då metallstaven sänks ned i vätskan. Har vi väl den kan vi enkelt räkna ut vätskans densitet då volymen av staven är känd. | ||
| + | |||
| + | Enheterna som är angivna i uppgiften, cm och g, är farliga att använda då vi riskerar att få decimalfel. Vi gör om dem till SI-enheter och sätter upp jämviktsekvationen kring nålen för krafter <math>F</math> och avstånd <math>d</math> enligt (obs M nedan för moment, ej massa M, uppgiftsförfattaren har medvetet valt en olämplig bokstav i uppgiftsformuleringen för att förvirra). | ||
| + | |||
| + | <math>M_{nål}: \sum_i d_i \cdot F_i = 0</math> | ||
| + | |||
| + | Med våra värden insatta har vi | ||
| + | |||
| + | <math>M_{nål}: | ||
| + | 3 \cdot 10^{-2} \cdot 0{,}1 \cdot 10^{-3} \cdot g | ||
| + | +7 \cdot 10^{-2} \cdot 1 \cdot 10^{-3} \cdot g | ||
| + | +8 \cdot 10^{-2} \cdot 10 \cdot 10^{-3} \cdot g | ||
| + | -10 \cdot 10^{-2} \cdot F_L</math> | ||
| + | |||
| + | Vi löser ut lyftkraften från nedsänkningen i vätskan, F_L ovan, till | ||
| + | |||
| + | <math>F_L = 8{,}73 \cdot 10^{-4} g</math> | ||
| + | |||
| + | Vi utgår från de båda sambanden <math>F = mg</math>, <math>\rho = \displaystyle\frac{m}{V}</math> | ||
| + | |||
| + | Vi söker <math>\rho</math> och löser ut det till <math>\rho = \displaystyle\frac{F_L}{gV}</math>. Med kraften <math>F_L)</math> och volymen <math> V= 10 \mbox{cm^3} = 10 \cdot (0{,}01^3 \mbox{m^3} = 1,00 \cdot 10^{-5} m^3</math> insatt får vi | ||
| + | |||
| + | <math>\rho = | ||
| + | \displaystyle\frac{8{,}73 \cdot 10^{-4} g}{gV} = | ||
| + | \displaystyle\frac{8{,}73 \cdot 10^{-4}}{10^{-5}} = 87,3 | ||
| + | </math> | ||
| + | |||
| + | Eftersom vi konsekvent använt SI-enheter utan prefix när vi räknat trillar också resultatet ut i detta format, densiteten är alltså <math>87,3 \mbox{kg/m}^3</math> | ||
| + | |||
| + | Är detta ett rimligt svar? De flesta vätskor har en dencitet mellan <math>700 - 3000 \mbox{kg/m}^3</math> varför svaret är något förvirrande.. antingen har vi gjort något räknefel någonstans eller så är uppgiften konstruerad utan tanke på ett verkligt fall. | ||
| + | |||
| + | <!--<font color=red>Uppdrag: kontrollera räkningar, om de är rätt, överväg att modifiera uppgiftsformuleringen, orimligt att resultatet är en vätska som ej finns!</font>--> | ||
| + | |||
====E4==== | ====E4==== | ||
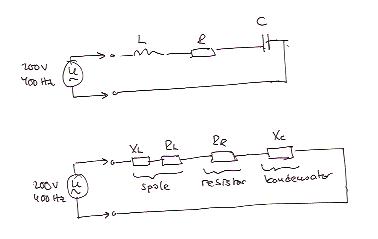
| + | Ett standardproblem i elläran, att beräkna impedansen vid en viss frekvens och därur ta reda på hur ström och spänning ser ut för kretsen. | ||
| + | |||
| + | Toppvärde eller effektivvärde? Vi inser att uppgiften är otydlig, vi vet inte om det var ett effektivvärde eller toppvärde som angavs för spänningen! Beräknningarna i sig blir identiska, de båda värdena skiljer sig enbart åt med en skalfaktor som i detta fall är <math>\sqrt{2}</math>. I ett praktiskt fall är det naturligtvis väldigt viktigt att veta vad det är för siffror vi utgår från, som en räkneövning kan vi faktiskt bortse från detta och helt enkelt säga att om spänningen var ett effektivvärde så har vi nu beräknat strömmens effektivvärde, om å andra sidan spänningen var ett toppvärde så har vi nu istället beräknat strömmens toppvärde. | ||
| + | |||
| + | |||
| + | [[Bild:Fysik_1_001.jpg]] | ||
| + | |||
| + | Spolen<br/> | ||
| + | <math>X_L = j\omega L = j 2 \pi \nu L = j 2 \pi \cdot 400 \cdot 0{,}05 \Omega \approx 125{,}6 \Omega</math> | ||
| + | |||
| + | <math>R_L =60 \, \Omega</math> | ||
| + | |||
| + | Resistorn<br/> | ||
| + | <math>R_R = 100 \,\Omega</math> | ||
| + | |||
| + | Kondensatorn<br/> | ||
| + | <math>X_C = \displaystyle\frac{1}{j \omega C} = \frac{1}{j 2\pi \nu C} = \frac{-j}{2 \pi \nu C} = -j\,\frac{1}{2 \pi \cdot 400 \cdot 4{,}0 \cdot 10^{-6}} = 99{,}5 \,\Omega</math> | ||
| + | |||
| + | Kretsens impedans beräknas med ett visardiagram (som i teorin) och vi får | ||
| + | |||
| + | [[Bild:Fysik_1_002.jpg]] | ||
| + | |||
| + | Ur detta ser vi att fasvinkeln kan beräknas som | ||
| + | |||
| + | [[Bild:Fysik_1_003.jpg]] | ||
| + | |||
| + | <math>\phi = arg(Z) = \arctan\displaystyle\frac{26{,}1}{160} \approx 9^\circ</math> | ||
| + | |||
| + | Och absolutbeloppet fås som | ||
| + | |||
| + | <math>|Z| = \sqrt{160^2 + 26{,}1^2}\, \Omega \approx 162 \, \Omega</math> | ||
| + | |||
| + | |||
| + | Sambandet mellan spänning och ström för en växelströmskrets ges av Ohms lag enligt | ||
| + | |||
| + | <math>u(t) = Z \cdot i(t)</math> | ||
| + | |||
| + | Vi löser ut strömmen som | ||
| + | |||
| + | |||
| + | <math>i(t) = \displaystyle\frac{u(t)}{Z}</math> och får att spänningen ligger <math>9^\circ</math> <u>före</u> strömmen (kretsen är strömtrög då den induktiva reaktansen är större än den kapacitiva). | ||
| + | |||
| + | Storleken på strömmen är <math>i(t) = \displaystyle\frac{200\, \mbox{V}}{126\, \Omega} \approx 1{,}6 \,\mbox{A} </math>. | ||
| + | |||
| + | |||
| + | |||
| + | |||
====E5==== | ====E5==== | ||
| + | |||
| + | Vi antar att lika stor energi förs över i samtliga urladdningar, ett alternativt scenario skulle kunna vara att det mesta av energin finns i den första urladdningen. | ||
| + | |||
| + | Om det är fem urladdningar och varje urladdning för över lika hög energi gäller för en urladdning | ||
| + | |||
| + | Utvecklad effekt <math>P = \displaystyle\frac{W}{t} = \frac{5 \mbox{C}}{10 \mu\mbox{s}} = 500 \mbox{MW} | ||
| + | |||
| + | Ström under genomslag <math>P = E J</math> där E är det elektriska fältet och J strömmen per areaenhet vilket kan förenklas till <math>P = U I </math> varvid vi kan lösa ut strömmen <math>I = \displaystyle\frac{P}{U} = \frac{500 \mbox{MW}}{100 \mbox{MV}} = 5 \mbox{A}</math> | ||
| + | |||
| + | Energitransporten <i>W</i> är given i uppgiftsformuleringen, 5 C under hela förloppet och enligt vårt antagande 1 C per urladdning. | ||
| + | |||
| + | Medeleffekten under ett blixtnedslag, enligt uppgiften pågår hela blixtnedslaget under 200 ms vid fem urladdningar, under denna tid förs energin 5 C över varför medeleffekten blir | ||
| + | |||
| + | <math>\bar{P} = \displaystyle\frac{5 \mbox{C}}{200 \mbox{ms}} = 25 \mbox{W}</math> | ||
| + | |||
| + | <!--<font color=red>Är detta vad som efterfrågas? Verkar vara väl trivial lösning... ställer mig också tveksam till att strömmen är så pass liten som beräkningarna visar, är fältstyrkan verkligen korrekt angiven för ett riktigt fall?</font>--> | ||
Nuvarande version
| Goda råd | Exempel uppgift |
Exempeluppgift
Detta är ett exempel på en inlämningsuppgift i Internetfysikkursen. Denna uppgift är alltså inte den inlämningsuppgift som du ska göra, utan den får du tillgång till först när du fått godkänt på alla slutprov.
Uppgifter
E1. Leta reda på tillverkarens tekniska produktfakta för en värmepump som marknadsförs för enfamiljshus. (Det finns mycket på webben.) Värmepumpars prestanda brukar anges för några olika driftsförhållanden med en viss standardtemperatur på den varma sidan och en viss standardtemperatur på den kalla sidan. (Det förklaras ofta i en liten fotnot till en tabell.) Du ska genomföra denna uppgift för en enda uppsättning temperaturer och inte för samtliga driftsförhållanden som förekommer på faktabladet.
- Identifiera effekter motsvarande \displaystyle Q_{\rm{varm}} och \displaystyle W_{\rm{in}} samt värmefaktorn \displaystyle COP_{\rm{vp}}. Var noga med mätenheter.Kontrollera att de givna värdena för dessa storheter överensstämmer med definitionen av värmefaktorn. (Eventuellt kan du tvärtom behöva beräkna den tredje storheten utifrån givna värden för enbart två storheter.)
- Beräkna den värmeeffekt som värmepumpen tar från den kalla sidan, t.ex. jord eller berggrund.
- Ger den andra huvudsatsen en möjlighet att beräkna en undre gräns, (\displaystyle COP_{\rm{vp}} > · · · ), ett exakt värde, (\displaystyle COP_{\rm{vp}} = · · · ), eller en övre gräns, (\displaystyle COP_{\rm{vp}} < · · · ), för värmefaktorn? Genomför denna uppskattning och jämför med pumpens verkliga värmefaktor.
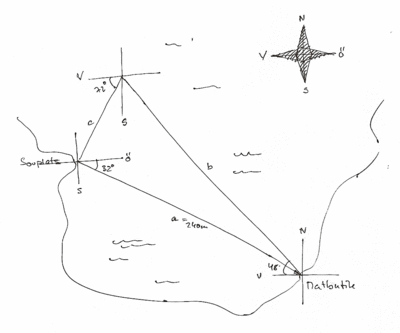
E2. Du är ute och paddlar kanot på en sjö. En morgon startar du från ditt nattläger vid stranden och paddlar först 240m i en riktning som ligger \displaystyle 32^{\circ} söder om riktningen rakt åt öster för att handla i en affär, vars läge du sett markerat på en karta. På kartan har du kunnat mäta ut den angivna längden.
När du paddlar tillbaka, så paddlar du först en sträcka \displaystyle b i en riktning som ligger \displaystyle 48^{\circ} norr om riktningen rakt åt väster; därefter paddlar du en sträcka \displaystyle c i en riktning som ligger \displaystyle 72^{\circ} söder om riktningen rakt åt väster, varefter du är tillbaka i lägret. Riktningarna mäter du med din kompass, men du vet inte längderna för de sträckor du paddlar på tillbakavägen.
Använd vektorer för att bestämma längderna \displaystyle b och \displaystyle c.
E3. En plastlinjal är drygt 20 cm lång. Vid markeringen för 10 cm finns ett hål i linjalen i vilket man kan sticka in t.ex. en stoppnål. Denna fungerar då som en axel kring vilken linjalen blir vridbar. En metallstav \displaystyle S och en motvikt \displaystyle M håller varandra i jämvikt, när de är placerade som i figuren. Båda hänger i mycket tunna trådar. Metallstavens volym är 10,0 cm\displaystyle ^3.
En bägare med vätska placeras så att metallstaven i sin helhet blir omgiven av vätskan. För att återställa jämvikten hänger man vid lämpliga skalstreck (se figuren nedan) små ståltrådar med massorna 0,1 g, 1 g och 10 g.
Bestäm vätskans densitet om, som i figuren, ståltrådarna måste hängas på avstånden 3 cm, 7 cm respektive 8 cm från vridningsaxeln.
E4. En elektrisk krets består av tre seriekopplade komponenter, en spole med resistansen 60\displaystyle \Omega och induktans 0,05 H, en resistor med resistansen 100\displaystyle \Omega samt en kondensator med kapacitansen 4,0 \displaystyle \muF. Kretsen ansluts till 200 V, 400 Hz. Beräkna strömmen i kretsen till belopp och fas i förhållande till spänningen.
E5. Ett blixtnedslag består i allmänhet av 4–5 urladdningar efter varandramedkorta mellanrum(50 ms). Antag att en av dessa urladdningar transporterar 5C över en potentialskillnad av 100MV mellan moln och mark under loppet av 10 μs. Beräkna den genomsnittliga strömmen, energitransporten och den genomsnittliga effekt som utvecklas.
Lösning
E1
E2
Vi har fått ett antal kompasskurser angivna och söker två sträckor.
Vi antar att vi använder en vanlig kompass med vinkelsumman \displaystyle 360^\circ på ett varv, vidare antar vi att avdrift och kompassdeviation mm är noll. Att göra sådana här antaganden är viktiga för att förenkla problemen till rimlig komplexitet.
Med dessa förenklingar så får vi ett problem med tre vektorer vars summa är noll, se illustration. Dessvärre är vinklarna angivna något egendomligt varför vi behöver göra om dessa till kartesiska koordinater i ett x-y-system. För att få rätt vinklar i rätt riktning så skissar vi problemställningen, en utmaning är ju att vinklarna är angivna relativt till olika väderstreck och inte relativt x-axeln!
Vi väljer att ha öst som x-koordinat (och därmed blir väst negativa x-koordinater) samt nord som y-koordinat (med syd som negativ y-koordinat). Andra val kan självklart göras, detta är kanske det mest intuitiva?
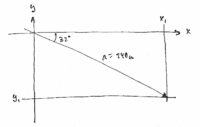
Vektorn a inlagd i detta koordinatsystem ger
\displaystyle \bar{a} = 240 ( \cos{32^\circ}\, , - \, \sin{32^\circ})
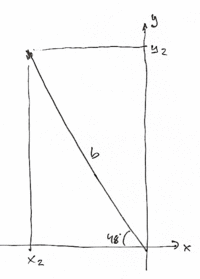
Vektorn b inlagd i samma koordinatsystemt ger
\displaystyle \bar{b} = b ( -\, \cos{48^\circ}\, , \,\sin{48^\circ} )
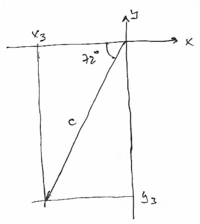
Vektorn c slutligen
\displaystyle \bar{c} = c (-\,\cos{72^\circ},-\,\sin{72^\circ} )
Vi tittar (som vanligt) på x- och y-värdena var för sig och får två ekvationer med totalt två obekanta. Lika många obekanta som antalet ekvationer, innebär att vi kan lösa problemet matematiskt såvida inte de två ekvationerna är identiska.
\displaystyle x: \quad 240 \cdot\cos(32^\circ) -\, b \cdot \cos(48^\circ) -\, c \cdot \cos(72^\circ) = 0
\displaystyle y: \quad -\,240 \cdot \sin(32^\circ) +b \cdot \sin(48^\circ)-\, c \cdot \sin(72^\circ) = 0
Vi inser att vi har ett ekvationssytem som är lösbart, vi löser det exakt nedan (du kan välja att först beräkna de trigometriska funktionernas värden med 3-4 värdesiffror men det kommer att ge avrundningsfel, hur stora?)
\displaystyle 240 \cdot\cos(32^\circ) -\, b \cdot \cos(48^\circ) -\, c \cdot \cos(72^\circ) = 0 (1)
\displaystyle -\,240 \cdot \sin(32^\circ) +b \cdot \sin(48^\circ)-\, c \cdot \sin(72^\circ) = 0 (2)
Vi eliminerar b genom att multiplicera (1) med \displaystyle \displaystyle\frac{\sin{48^\circ}}{\cos{48^\circ}} = \tan{48^\circ}
\displaystyle 240 \cdot\cos(32^\circ)\cdot \tan{48^\circ} -\, b \cdot \sin{48^\circ} -\, c \cdot \cos(72^\circ)\cdot \tan{48^\circ} = 0 (1)
\displaystyle -\,240 \cdot \sin(32^\circ) +b \cdot \sin(48^\circ)-\, c \cdot \sin(72^\circ) = 0 (2)
Vi adderar (1) och (2) och får
\displaystyle 240 \left( \cos{32}\cdot \tan{48} - \sin{32} \right) = c\left( \cos{72}\cdot \tan{48} + \sin{72} \right)
\displaystyle \Rightarrow c = 240 \cdot \displaystyle\frac{\cos{32}\cdot \tan{48} - \sin{23}}{\cos{72}\cdot\tan{48}+ \sin{72}} \approx 76
Det exakta värdet av c insatt i (1) överst ger b enligt
\displaystyle 240 \cdot \cos{32} - 240 \cdot \cos{72} \displaystyle\frac{\cos{32}\cdot\tan{48}-\sin{32}}{\cos{72} \cdot \tan{48} + \sin{72}}
\displaystyle \Rightarrow b = \displaystyle\frac{240}{\cos{48}} \cdot \left( \cos{32} - \cos{72} \displaystyle\frac{\cos{32}\cdot\tan{48}-\sin{32}}{\cos{72} \cdot \tan{48} + \sin{72}} \right) \approx 269
E3
Vi antar att det snöre som den stora metallstaven hänger i har massan noll och är styvt. Det innebär att det inte påverkar jämviktsekvationen och att en eventuell kraft riktad uppåt på metallstaven kommer att innebära att linjalen rör sig uppåt. Med detta antagande kan problemet lösas.
Vid en första anblick ser det ut som att vi ska sätta upp en jämviktsekvation för de två fallen och utifrån det plocka fram de obekanta massorna. Man inser ganska snart att detta inte hjälper, vi får fler obekanta än antalet ekvationer. Vi har inte heller så stor nytta av att få reda på de absoluta massorna för M och S i figuren.
Den huvudsakliga skillnaden mellan de båda fallen är att metallstaven i det senare är nedsänkt i en vätska. Vi misstänker att Archimedes princip kan vara användbar och drar oss den till minnes:
Archimedes princip
Lyftkraften på ett föremål i en vätska är lika stor som tyngden av den undanträngda vätskan.
Om vi sätter upp en jämviktsekvation kring knappnålen för skillnaden mellan fall 1 och fall 2 bör vi kunna få ut lyftkraften \displaystyle F_L som uppstår då metallstaven sänks ned i vätskan. Har vi väl den kan vi enkelt räkna ut vätskans densitet då volymen av staven är känd.
Enheterna som är angivna i uppgiften, cm och g, är farliga att använda då vi riskerar att få decimalfel. Vi gör om dem till SI-enheter och sätter upp jämviktsekvationen kring nålen för krafter \displaystyle F och avstånd \displaystyle d enligt (obs M nedan för moment, ej massa M, uppgiftsförfattaren har medvetet valt en olämplig bokstav i uppgiftsformuleringen för att förvirra).
\displaystyle M_{nål}: \sum_i d_i \cdot F_i = 0
Med våra värden insatta har vi
\displaystyle M_{nål}: 3 \cdot 10^{-2} \cdot 0{,}1 \cdot 10^{-3} \cdot g +7 \cdot 10^{-2} \cdot 1 \cdot 10^{-3} \cdot g +8 \cdot 10^{-2} \cdot 10 \cdot 10^{-3} \cdot g -10 \cdot 10^{-2} \cdot F_L
Vi löser ut lyftkraften från nedsänkningen i vätskan, F_L ovan, till
\displaystyle F_L = 8{,}73 \cdot 10^{-4} g
Vi utgår från de båda sambanden \displaystyle F = mg, \displaystyle \rho = \displaystyle\frac{m}{V}
Vi söker \displaystyle \rho och löser ut det till \displaystyle \rho = \displaystyle\frac{F_L}{gV}. Med kraften \displaystyle F_L) och volymen \displaystyle V= 10 \mbox{cm^3} = 10 \cdot (0{,}01^3 \mbox{m^3} = 1,00 \cdot 10^{-5} m^3 insatt får vi
\displaystyle \rho = \displaystyle\frac{8{,}73 \cdot 10^{-4} g}{gV} = \displaystyle\frac{8{,}73 \cdot 10^{-4}}{10^{-5}} = 87,3
Eftersom vi konsekvent använt SI-enheter utan prefix när vi räknat trillar också resultatet ut i detta format, densiteten är alltså \displaystyle 87,3 \mbox{kg/m}^3
Är detta ett rimligt svar? De flesta vätskor har en dencitet mellan \displaystyle 700 - 3000 \mbox{kg/m}^3 varför svaret är något förvirrande.. antingen har vi gjort något räknefel någonstans eller så är uppgiften konstruerad utan tanke på ett verkligt fall.
E4
Ett standardproblem i elläran, att beräkna impedansen vid en viss frekvens och därur ta reda på hur ström och spänning ser ut för kretsen.
Toppvärde eller effektivvärde? Vi inser att uppgiften är otydlig, vi vet inte om det var ett effektivvärde eller toppvärde som angavs för spänningen! Beräknningarna i sig blir identiska, de båda värdena skiljer sig enbart åt med en skalfaktor som i detta fall är \displaystyle \sqrt{2}. I ett praktiskt fall är det naturligtvis väldigt viktigt att veta vad det är för siffror vi utgår från, som en räkneövning kan vi faktiskt bortse från detta och helt enkelt säga att om spänningen var ett effektivvärde så har vi nu beräknat strömmens effektivvärde, om å andra sidan spänningen var ett toppvärde så har vi nu istället beräknat strömmens toppvärde.
Spolen
\displaystyle X_L = j\omega L = j 2 \pi \nu L = j 2 \pi \cdot 400 \cdot 0{,}05 \Omega \approx 125{,}6 \Omega
\displaystyle R_L =60 \, \Omega
Resistorn
\displaystyle R_R = 100 \,\Omega
Kondensatorn
\displaystyle X_C = \displaystyle\frac{1}{j \omega C} = \frac{1}{j 2\pi \nu C} = \frac{-j}{2 \pi \nu C} = -j\,\frac{1}{2 \pi \cdot 400 \cdot 4{,}0 \cdot 10^{-6}} = 99{,}5 \,\Omega
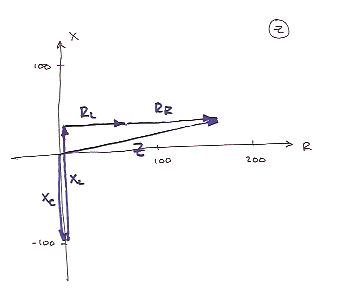
Kretsens impedans beräknas med ett visardiagram (som i teorin) och vi får
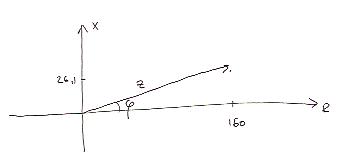
Ur detta ser vi att fasvinkeln kan beräknas som
\displaystyle \phi = arg(Z) = \arctan\displaystyle\frac{26{,}1}{160} \approx 9^\circ
Och absolutbeloppet fås som
\displaystyle |Z| = \sqrt{160^2 + 26{,}1^2}\, \Omega \approx 162 \, \Omega
Sambandet mellan spänning och ström för en växelströmskrets ges av Ohms lag enligt
\displaystyle u(t) = Z \cdot i(t)
Vi löser ut strömmen som
\displaystyle i(t) = \displaystyle\frac{u(t)}{Z} och får att spänningen ligger \displaystyle 9^\circ före strömmen (kretsen är strömtrög då den induktiva reaktansen är större än den kapacitiva).
Storleken på strömmen är \displaystyle i(t) = \displaystyle\frac{200\, \mbox{V}}{126\, \Omega} \approx 1{,}6 \,\mbox{A} .
E5
Vi antar att lika stor energi förs över i samtliga urladdningar, ett alternativt scenario skulle kunna vara att det mesta av energin finns i den första urladdningen.
Om det är fem urladdningar och varje urladdning för över lika hög energi gäller för en urladdning
Utvecklad effekt \displaystyle P = \displaystyle\frac{W}{t} = \frac{5 \mbox{C}}{10 \mu\mbox{s}} = 500 \mbox{MW}
Ström under genomslag
Energitransporten W är given i uppgiftsformuleringen, 5 C under hela förloppet och enligt vårt antagande 1 C per urladdning.
Medeleffekten under ett blixtnedslag, enligt uppgiften pågår hela blixtnedslaget under 200 ms vid fem urladdningar, under denna tid förs energin 5 C över varför medeleffekten blir
\displaystyle \bar{P} = \displaystyle\frac{5 \mbox{C}}{200 \mbox{ms}} = 25 \mbox{W}