Testsida
Förberedande kurs i matematik
| (23 mellanliggande versioner visas inte.) | |||
| Rad 106: | Rad 106: | ||
</div>{{#NAVCONTENT:Svar| Svar 1.5.1 | Lösning 1.5.1.a | Lösning 1.5.1.a | Lösning 1.5.1.b | | </div>{{#NAVCONTENT:Svar| Svar 1.5.1 | Lösning 1.5.1.a | Lösning 1.5.1.a | Lösning 1.5.1.b | | ||
Lösning 1.5.1.b}} | Lösning 1.5.1.b}} | ||
| + | |||
| + | ===Övning 1.8.1 === | ||
| + | <div class="ovning"> | ||
| + | {| width="100%" cellspacing="10px" | ||
| + | |Förenkla <math> (1+i)^{2012}-(1-i)^{2012} </math> | ||
| + | || | ||
| + | |} | ||
| + | </div>{{#NAVCONTENT:Svar| Svar 1.8.1 | Lösning 1.8.1 | Lösning 1.8.1}} | ||
| + | |||
| + | |||
| + | ===Övning 1.8.2 === | ||
| + | <div class="ovning"> | ||
| + | {| width="100%" cellspacing="10px" | ||
| + | |Antag att vi definierar en sekvens av komplexa tal genom <math>z_1 =0 </math> | ||
| + | och <math> z_{n+1}=z^2_n+i </math> för <math> n \geq 1</math>. Hur långt från origo kommer då <math> z_{111} </math> befinna sig? (Källa: AHSME) | ||
| + | || | ||
| + | |} | ||
| + | </div>{{#NAVCONTENT:Svar| Svar 1.8.2 | Lösning 1.8.2 | Lösning 1.8.2}} | ||
| + | |||
| + | ===Övning 1.8.3 === | ||
| + | <div class="ovning"> | ||
| + | {| width="100%" cellspacing="10px" | ||
| + | |För heltalsvärden på n, vilka värden kan <math> i^n+i^{-n}</math> anta? | ||
| + | || | ||
| + | |} | ||
| + | </div>{{#NAVCONTENT:Svar| Svar 1.8.3 | Lösning 1.8.3 | Lösning 1.8.3}} | ||
| + | |||
| + | ===Övning 1.8.5 === | ||
| + | <div class="ovning"> | ||
| + | {|width="100%" cellspacing="10px" | ||
| + | | a) | ||
| + | | Är <math> \sqrt{2} </math> ett reellt eller komplext tal? | ||
| + | | b) | ||
| + | | Är <math>3+3i </math> ett reellt eller ett komplext tal? | ||
| + | | c) | ||
| + | | Hitta alla komplexa rötter till <math>p(z) = z^3+z=0 </math>. Hur många reella rötter har <math>p(z)</math> Hur många komplexa rötter har den? | ||
| + | Kan en funktion ha fler reella än komplexa rötter? | ||
| + | |||
| + | || | ||
| + | |} | ||
| + | </div>{{#NAVCONTENT:Svar | Svar 1.8.5 | Lösning 1.8.5a | Lösning 1.8.5a | Lösning 1.8.5b | Lösning 1.8.5b | Lösning 1.8.5c | Lösning 1.8.5c }} | ||
| + | ===Övning 1.9.1 === | ||
| + | <div class="ovning"> | ||
| + | {| width="100%" cellspacing="10px" | ||
| + | |a) | ||
| + | |Utveckla<math> (x+y)²-(x-y)² </math> | ||
| + | |b) | ||
| + | | Använd ovanstående för att beräkna <math> 46 \cdot 54</math>. | ||
| + | || | ||
| + | |} | ||
| + | </div>{{#NAVCONTENT:Svar| Svar 1.9.1 | Lösning 1.9.1.a | Lösning 1.9.1.a | Lösning 1.9.1.b | Lösning 1.9.1.b}} | ||
| + | |||
| + | ===Övning 1.8.6=== | ||
| + | <div class="ovning"> | ||
| + | {|width="100%" cellspacing="10px" | ||
| + | | Låt <math>z=a+bi</math>. Vi vet att <math>z/(3+4i)=2+i</math>. Bestäm <math> a </math> och <math> b</math>. | ||
| + | |||
| + | || | ||
| + | |} | ||
| + | </div>{{#NAVCONTENT:Svar | Svar 1.8.6 | Lösning 1.8.6 | Lösning 1.8.6}} | ||
| + | |||
| + | |||
| + | |||
| + | ===Övning 1.9.1 === | ||
| + | <div class="ovning"> | ||
| + | {| width="100%" cellspacing="10px" | ||
| + | |a) | ||
| + | |Utveckla<math> (x+y)²-(x-y)² </math> | ||
| + | |b) | ||
| + | | Använd ovanstående för att beräkna <math> 46 \cdot 54</math>. | ||
| + | || | ||
| + | |} | ||
| + | </div>{{#NAVCONTENT:Svar| Svar 1.9.1 | Lösning 1.9.1.a | Lösning 1.9.1.a | Lösning 1.9.1.b | Lösning 1.9.1.b}} | ||
| Rad 127: | Rad 200: | ||
</div>{{#NAVCONTENT:Svar| Svar 2.1.1| Lösning 2.1.1a | Lösning 2.1.1a | Lösning 2.1.1b | | </div>{{#NAVCONTENT:Svar| Svar 2.1.1| Lösning 2.1.1a | Lösning 2.1.1a | Lösning 2.1.1b | | ||
Lösning 2.1.1b | Lösning 2.1.1c | Lösning 2.1.1c | Lösning 2.1.1d | Lösning 2.1.1d | Lösning 2.1.1e | Lösning 2.1.1e }} | Lösning 2.1.1b | Lösning 2.1.1c | Lösning 2.1.1c | Lösning 2.1.1d | Lösning 2.1.1d | Lösning 2.1.1e | Lösning 2.1.1e }} | ||
| + | |||
| + | |||
| + | ===Övning 3.2.1 === | ||
| + | <div class="ovning"> | ||
| + | Låt <math>f(x)=5x</math>. Bestäm <math>f</math>:s värdemängd och avgör huruvida | ||
| + | <math>f</math> är injektiv/surjektiv i vart och ett av följande fall: | ||
| + | |||
| + | {| width="100%" cellspacing="10px" | ||
| + | |a) | ||
| + | |<math> f:\{3,5,6,7\} \to \mathbb{R} </math> | ||
| + | |b) | ||
| + | | <math> f:\mathbb{R}\to \mathbb{R} </math> | ||
| + | | c) | ||
| + | | <math> f:\mathbb{R}\to \mathbb{C} </math> | ||
| + | | d) | ||
| + | | <math> f:\mathbb{Z}\to \mathbb{Z} </math> | ||
| + | || | ||
| + | |} | ||
| + | </div>{{#NAVCONTENT:Svar| Svar 3.2.1 | Lösning 3.2.1.a | Lösning 3.2.1.a | Lösning 3.2.1.b | Lösning 3.2.1.b | Lösning 3.2.1.c | Lösning 3.2.1.c | Lösning 3.2.1.d | Lösning 3.2.1.d}} | ||
| + | |||
| + | ===Övning 3.2.2=== | ||
| + | <div class="ovning"> | ||
| + | {| width="100%" cellspacing="10px" | ||
| + | Vissa funktioner har egenskapen att de är både injektiva och surjektiva, och vi kallar dessa funktioner bijektiva. En egenskap hos bijektiva funktioner är att målmängden och definitionsmängden innehåller precis lika många element. Detta är lätt att se med funktioner definierade på ändliga mängder, men samma resonemang används av matematiker för oändliga mängder. Vi säger då att två mängder har samma kardinalitet om och endast om vi kan skapa en bijektion mellan dem. Detta leder till lite märkliga samband. För att belysa ett av dem: | ||
| + | | | ||
| + | Kan man skapa en bijektion mellan de naturliga talen <math>\mathbb{N}</math> och heltalen <math>\mathbb{Z}</math>? | ||
| + | |}</div>{{#NAVCONTENT:Svar| Svar 3.2.2 | Lösning 3.2.2 | Lösning 3.2.2}} | ||
| + | |||
| + | ===Övning 3.2.4=== | ||
| + | <div class="ovning"> | ||
| + | I kurslitteraturen beskrivs injektivitet som att en funktion <math>f:{T}\rightarrow{S}</math> är injektiv om f avbildar "skilda värden på skilda värden". Detta kan man tolka som att <math>a \neq b \Rightarrow f(a) \neq f(b)</math>. Detta påstående är däremot inte alltid så praktiskt att arbeta med. En enklare formulering är det ekvivalenta <math> f(a)=f(b) \Rightarrow a = b</math> . Vi kan läsa ut denna formulering som att "om avbildningen av två element är samma, så måste de två elementen också vara samma". | ||
| + | |||
| + | Använd <math> f(a)=f(b) \Rightarrow a = b</math> för att visa att följande funktioner är injektiva. Låt <math>f, g, h, p:{R} \to {R}</math> | ||
| + | |||
| + | |||
| + | a) <math>f(x) = 4x + 5 </math> | ||
| + | |||
| + | b) <math>g(x) = x^3 </math> | ||
| + | |||
| + | c) <math>h(x) = e^{x}</math> | ||
| + | |||
| + | d) <math>p(x) = h(g(x))</math> | ||
| + | |||
| + | </div>{{#NAVCONTENT:Lösning a)| Lösning 3.2.4a | Lösning b) | Lösning 3.2.4b | Lösning c) | Lösning 3.2.4c | Lösning d) | Lösning 3.2.4d}} | ||
| Rad 134: | Rad 251: | ||
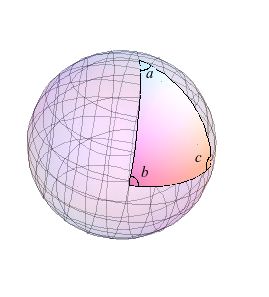
|Gäller Pythagoras sats för trianglar ritade på en sfär? | |Gäller Pythagoras sats för trianglar ritade på en sfär? | ||
|| | || | ||
| + | [[Bild:Triangel.jpg]] | ||
|} | |} | ||
</div>{{#NAVCONTENT:Svar| Svar 3.5.1 | Lösning 3.5.1 | Lösning 3.5.1}} | </div>{{#NAVCONTENT:Svar| Svar 3.5.1 | Lösning 3.5.1 | Lösning 3.5.1}} | ||
| + | ===Övning 4.1.1 === | ||
| + | <div class="ovning"> | ||
| + | Beräkna följande gränsvärden. | ||
| + | {| width="100%" cellspacing="10px" | ||
| + | |a) | ||
| + | | <math>\lim_{x\to 0}3 </math> | ||
| + | | b) | ||
| + | | <math> \lim_{x\to 0}\frac{x}{x^2} </math> | ||
| + | | c) | ||
| + | | <math> \lim_{x\to 0}\frac{x}{x} </math> | ||
| + | | d) | ||
| + | | <math> \lim_{x\to \infty}\frac{x^2+3}{x^3+1} </math> | ||
| + | | e) | ||
| + | | <math> lim_{x\to 0}\frac{2x^3+x^2+1}{x^3+1} </math> | ||
| + | || | ||
| + | |} | ||
| + | </div>{{#NAVCONTENT:Svar | Svar 4.1.1 | Lösning 4.1.1.a | Lösning 4.1.1.a | Lösning 4.1.1.b | Lösning 4.1.1.b | Lösning 4.1.1.c | Lösning 4.1.1.c | Lösning 4.1.1.d | Lösning 4.1.1.d | Lösning 4.1.1.e | Lösning 4.1.1.e }} | ||
===Övning 4.2.1=== | ===Övning 4.2.1=== | ||
| Rad 152: | Rad 287: | ||
Lösning 4.2.1.b | Lösning 4.2.1.c | Lösning 4.2.1.c}} | Lösning 4.2.1.b | Lösning 4.2.1.c | Lösning 4.2.1.c}} | ||
| + | ===Övning 4.3.1=== | ||
| + | <div class="ovning"> | ||
| + | {| width="100%" cellspacing="10px" | ||
| + | | a) | ||
| + | |Visa att <math>-\ln(\cos x)</math> är en primitiv funktion till <math>\sin x/\cos x.</math> | ||
| + | | b) | ||
| + | | Visa att <math>x\ln(x) -x</math> är en primitiv funktion till <math>\ln (x).</math> | ||
| + | | | ||
| + | || | ||
| + | |} | ||
| + | </div>{{#NAVCONTENT:Svar| Svar 4.3.1 | Lösning 4.3.1.a | Lösning 4.3.1.a | Lösning 4.3.1.b | | ||
| + | Lösning 4.3.1.b}} | ||
| - | \section{Kapitel 2} | ||
| - | {Logik} | ||
| - | \subsubsection{ } | ||
| - | Bestäm vilka av följande påståenden som är sanna för reella tal <math>x</math>. | ||
| - | \begin{list}{ }{ } | ||
| - | \item a) <math>x>2 \Rightarrow x\geq -1</math> | ||
| - | \item b) <math>x >2 \Leftarrow x \geq -1</math> | ||
| - | \item c) <math>x\geq 0\wedge x>1\Leftrightarrow x >1</math> | ||
| - | \item d) <math>x\geq 0 \Rightarrow x^2\geq 0</math> | ||
| - | \item e) <math>x^2<0 \Rightarrow x^2\geq 0</math> | ||
| - | \end{list} | ||
| - | Exempellösningar: | ||
| - | a) Vi vet att <math>2</math> är större än <math>-1</math>. Om vi har ett <math>x</math> som är större än <math>2</math> så vet vi att det också måste vara större än <math>-1</math>. Det är just precis detta som den logiska formeln betyder och alltså är den sann. | ||
| - | + | ===Övning 4.3.2=== | |
| + | <div class="ovning"> | ||
| + | Antag att vi har två deriverbara funktioner f och g så att f(x)=0 för alla x. | ||
| + | {| width="100%" cellspacing="10px" | ||
| + | | a) | ||
| + | |Skriv upp en formel för derivatan av <math>f(x)^{g(x)}</math> uttryckt i <math>D(f(x))</math> och <math>D(g(x)).</math> | ||
| + | | b) | ||
| + | | Tillämpa formeln genom att derivera <math>(x^2+1)^3.</math> | ||
| + | | c) | ||
| + | | Derivera <math>x^x</math> då <math>x>0</math>. | ||
| + | | d) | ||
| + | | Derivera <math>x^{\sin x}</math> då <math>x>0</math>. | ||
| + | || | ||
| + | |} | ||
| + | </div>{{#NAVCONTENT:Svar| Svar 4.3.2 | Lösning 4.3.2.a | Lösning 4.3.2.a | Lösning 4.3.2.b | | ||
| + | Lösning 4.3.2.b | Lösning 4.3.2.c | Lösning 4.3.2.c | Lösning 4.3.2.d | Lösning 4.3.2.d}} | ||
| - | + | ===Övning 4.3.3=== | |
| + | <div class="ovning"> | ||
| + | {| width="100%" cellspacing="10px" | ||
| + | | a) | ||
| + | | Derivera <math>\sin x /x</math>. | ||
| + | | b) | ||
| + | | Derivera <math>\sin^3x + 3\sin x \cos x.</math> | ||
| + | | | ||
| + | || | ||
| + | |} | ||
| + | </div>{{#NAVCONTENT:Svar| Svar 4.3.3 | Lösning 4.3.3.a | Lösning 4.3.3.a | Lösning 4.3.3.b | | ||
| + | Lösning 4.3.3.b}} | ||
| - | + | ===Övning 4.3.4=== | |
| + | <div class="ovning"> | ||
| + | Våra produkt- och kvotregler för derivation är förvisso praktiska och tydliga. Emellanåt stöter man däremot på ett uttryck som verkar skrivet av någon särskilt sadistisk lärare. | ||
| - | + | Ett exempel följer: | |
| - | \ | + | <math> y = \frac{abc}{de} </math> |
| - | { | + | |
| - | + | Där a, b, c, d, e är deriverbara, men knepiga, funktioner av x. | |
| - | + | Vad är då <math>\frac{dy}{dx}</math>? Finns det något smidigare sätt att lösa uppgiften på än upprepad använding av våra regler? | |
| - | + | ||
| - | + | </div>{{#NAVCONTENT: Lösning | Lösning 4.3.4}} | |
| - | + | ||
| - | + | ||
| - | { | + | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ===Övning 4.3.5=== | |
| - | + | <div class="ovning"> | |
| - | + | Implicit derivering går att använda till mer än jobbiga produkter. Tycker man att det är kämpigt att memorera derivator eller att ta till h-derivatan så kan vi använda denna metod istället när vi vill ta fram inversa derivator. | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | h | + | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| + | Kom ihåg hur vi använde kedjeregeln i föregående uppgift, och försök härleda derivatan till y=arcsin(x). Antag att vi redan vet derivatan för sin(x). | ||
| - | + | </div>{{#NAVCONTENT:Lösning | Lösning 4.3.5}} | |
| - | + | ||
| - | + | ||
Nuvarande version
Övning 1
Beräkna
| a) | \displaystyle \displaystyle(-3)(7+(-5)(-3+2)) | b) | \displaystyle \displaystyle (-a+2b)(-a+3b) |
Övning 2
Beräkna
| a) | Betrakta operationen \displaystyle a \bigstar b = a+2b. Är operationen kommutativ? (En operation är kommutativ den har egenskapen att \displaystyle a \bigstar b = b \bigstar a) | b) | Ge ett exempel på en operation som inte är associativ. (En operation är associativ om den har egenskapen att \displaystyle (a\bigstar b)\bigstar c=a\bigstar(b\bigstar c)) | c) | Ge ett exempel på en operation som inte är distributiv över addition. (En operation är distributiv över addition om \displaystyle a\bigstar(b+c)=a\bigstar b + a\bigstar c) |
Övning 1.2.1
Primtalsfaktorisera
| a) | \displaystyle \displaystyle 1024 | b) | \displaystyle \displaystyle 1331 |
Övning 1.2.2
Hur många äkta delare har 23?
Övning 1.4.1
| a) | Beräkna \displaystyle 38800\cdot5 modulo 3. | b) | Beräkna entalssiffran i talet \displaystyle 37^{120}. |
Övning 1.4.2
| a) | Ett tal är jämnt delbart med två precis då dess entalssiffra är delbar med två. Bevisa detta med hjälp av moduloräkning. | b) | Ett heltals siffersumma är summan av siffrorna i talet. Till exempel är siffersumman av 354 lika med 3+5+4=12.Ett tal är jämnt delbart med tre precis då dess siffersumma är jämnt delbar med tre. Bevisa detta med hjälp av moduloräkning. |
Övning 1.4.3
| a) | Ett tal är jämnt delbart med 5 precis då dess entalssiffra antingen är 0 eller 5. Bevisa detta med hjälp av moduloräkning. | b) | En alternerande siffersumma för ett tal är summan av siffrorna med växlande tecken. Till exempel är siffersumman hos 35478 lika med \displaystyle 3-5+4-7+8=-1. Ett tal är jämnt delbart med 11 precis då dess alternerande siffersumma är delbar med 11. Bevisa detta med hjälp av moduloräkning. |
{Moduloräkning}
Övning 1.5.1
| a) | Konvertera talet \displaystyle 201_3 till bas 4. | b) | Det går att använda sig av baser högre än 10: till exempel kan vi räkna i basen elva. Då kommer vi behöva en symbol som representerar värdet 10 (här kan vi till exempel använda oss av symbolen \displaystyle \bigstar). Systemet fungerar precis likadant som för baser under tio: till exempel kan vi konvertera talet \displaystyle 13\bigstar02_{11} till basen 10 genom att räkna följande: \displaystyle 1*11^4+3*11^3+10*11^2+0*11^1+2*11^0=19846.
Konvertera nu talet \displaystyle 252_{10} till basen 11. |
Övning 1.8.1
| Förenkla \displaystyle (1+i)^{2012}-(1-i)^{2012} |
Övning 1.8.2
| Antag att vi definierar en sekvens av komplexa tal genom \displaystyle z_1 =0
och \displaystyle z_{n+1}=z^2_n+i för \displaystyle n \geq 1. Hur långt från origo kommer då \displaystyle z_{111} befinna sig? (Källa: AHSME) |
Övning 1.8.3
| För heltalsvärden på n, vilka värden kan \displaystyle i^n+i^{-n} anta? |
Övning 1.8.5
| a) | Är \displaystyle \sqrt{2} ett reellt eller komplext tal? | b) | Är \displaystyle 3+3i ett reellt eller ett komplext tal? | c) | Hitta alla komplexa rötter till \displaystyle p(z) = z^3+z=0 . Hur många reella rötter har \displaystyle p(z) Hur många komplexa rötter har den?
Kan en funktion ha fler reella än komplexa rötter? |
Övning 1.9.1
| a) | Utveckla\displaystyle (x+y)²-(x-y)² | b) | Använd ovanstående för att beräkna \displaystyle 46 \cdot 54. |
Övning 1.8.6
| Låt \displaystyle z=a+bi. Vi vet att \displaystyle z/(3+4i)=2+i. Bestäm \displaystyle a och \displaystyle b. |
Övning 1.9.1
| a) | Utveckla\displaystyle (x+y)²-(x-y)² | b) | Använd ovanstående för att beräkna \displaystyle 46 \cdot 54. |
Övning 2.1
Bestäm vilka av följande påståenden som är sanna för reella tal \displaystyle x.
| a) | \displaystyle x>2 \Rightarrow x\geq -1 | b) | \displaystyle x >2 \Leftarrow x \geq -1 | |||
| c) | \displaystyle x\geq 0\wedge x>1\Leftrightarrow x >1 | d) | \displaystyle x\geq 0 \Rightarrow x^2\geq 0 | e) | \displaystyle x^2<0 \Rightarrow x^2\geq 0 |
Övning 3.2.1
Låt \displaystyle f(x)=5x. Bestäm \displaystyle f:s värdemängd och avgör huruvida \displaystyle f är injektiv/surjektiv i vart och ett av följande fall:
| a) | \displaystyle f:\{3,5,6,7\} \to \mathbb{R} | b) | \displaystyle f:\mathbb{R}\to \mathbb{R} | c) | \displaystyle f:\mathbb{R}\to \mathbb{C} | d) | \displaystyle f:\mathbb{Z}\to \mathbb{Z} |
Övning 3.2.2
|
Kan man skapa en bijektion mellan de naturliga talen \displaystyle \mathbb{N} och heltalen \displaystyle \mathbb{Z}? |
Övning 3.2.4
I kurslitteraturen beskrivs injektivitet som att en funktion \displaystyle f:{T}\rightarrow{S} är injektiv om f avbildar "skilda värden på skilda värden". Detta kan man tolka som att \displaystyle a \neq b \Rightarrow f(a) \neq f(b). Detta påstående är däremot inte alltid så praktiskt att arbeta med. En enklare formulering är det ekvivalenta \displaystyle f(a)=f(b) \Rightarrow a = b . Vi kan läsa ut denna formulering som att "om avbildningen av två element är samma, så måste de två elementen också vara samma".
Använd \displaystyle f(a)=f(b) \Rightarrow a = b för att visa att följande funktioner är injektiva. Låt \displaystyle f, g, h, p:{R} \to {R}
a) \displaystyle f(x) = 4x + 5
b) \displaystyle g(x) = x^3
c) \displaystyle h(x) = e^{x}
d) \displaystyle p(x) = h(g(x))
Övning 3.5.1
Övning 4.1.1
Beräkna följande gränsvärden.
| a) | \displaystyle \lim_{x\to 0}3 | b) | \displaystyle \lim_{x\to 0}\frac{x}{x^2} | c) | \displaystyle \lim_{x\to 0}\frac{x}{x} | d) | \displaystyle \lim_{x\to \infty}\frac{x^2+3}{x^3+1} | e) | \displaystyle lim_{x\to 0}\frac{2x^3+x^2+1}{x^3+1} |
Övning 4.2.1
| a) | Visa att \displaystyle D(x^2)=2x med hjälp av produktregeln. | b) | Visa att \displaystyle D(x^n)= nx^{n-1} om vi antar att man vet \displaystyle D(x^{n-1})=(n-1)x^{n-2}. | c) | Med hjälp av b), visa att \displaystyle D(x^n)=nx^{n-1} för alla \displaystyle n. |
Övning 4.3.1
| a) | Visa att \displaystyle -\ln(\cos x) är en primitiv funktion till \displaystyle \sin x/\cos x. | b) | Visa att \displaystyle x\ln(x) -x är en primitiv funktion till \displaystyle \ln (x). |
Övning 4.3.2
Antag att vi har två deriverbara funktioner f och g så att f(x)=0 för alla x.
| a) | Skriv upp en formel för derivatan av \displaystyle f(x)^{g(x)} uttryckt i \displaystyle D(f(x)) och \displaystyle D(g(x)). | b) | Tillämpa formeln genom att derivera \displaystyle (x^2+1)^3. | c) | Derivera \displaystyle x^x då \displaystyle x>0. | d) | Derivera \displaystyle x^{\sin x} då \displaystyle x>0. |
Övning 4.3.3
| a) | Derivera \displaystyle \sin x /x. | b) | Derivera \displaystyle \sin^3x + 3\sin x \cos x. |
Övning 4.3.4
Våra produkt- och kvotregler för derivation är förvisso praktiska och tydliga. Emellanåt stöter man däremot på ett uttryck som verkar skrivet av någon särskilt sadistisk lärare.
Ett exempel följer: \displaystyle y = \frac{abc}{de}
Där a, b, c, d, e är deriverbara, men knepiga, funktioner av x.
Vad är då \displaystyle \frac{dy}{dx}? Finns det något smidigare sätt att lösa uppgiften på än upprepad använding av våra regler?
Övning 4.3.5
Implicit derivering går att använda till mer än jobbiga produkter. Tycker man att det är kämpigt att memorera derivator eller att ta till h-derivatan så kan vi använda denna metod istället när vi vill ta fram inversa derivator.
Kom ihåg hur vi använde kedjeregeln i föregående uppgift, och försök härleda derivatan till y=arcsin(x). Antag att vi redan vet derivatan för sin(x).
 Hämtar...
Hämtar...