12.2 Gram-Schmidt ortogonaliseringsprocess
SamverkanLinalgLIU
| 12.1 | 12.2 | 12.3 |
Läs textavsnitt 12.2 Gram-Schmidt ortogonaliseringsprocess.
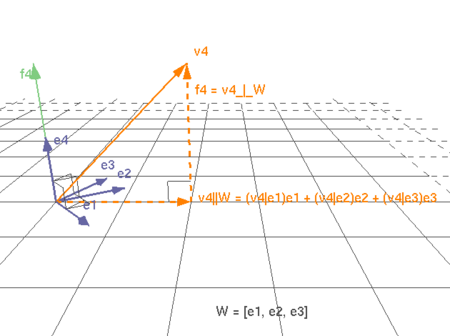
Innan Du börjar arbeta med detta moment så kan Du visualisera Gram-Schmidt ortogonaliseringsprocess genom att klicka på bilden.
Innehåll |
Övning 13.9
Bestäm en ON-bas för underrummet \displaystyle W=[(2,1,0,1)^t,(4,-5,1,3)^t]\subset{\bf R}^4 .
Övning 13.10
Låt
W=[(1,2,1,-1)^t,(1,0,1,0)^t]\subset{\bf E}^4.
Dela upp \displaystyle \boldsymbol{u}=(1,1,1,1)^t i en summa av två vektorer där den ena ligger i \displaystyle W och den andra är ortogonal mot \displaystyle W .
Övning 13.11
Låt
W=[(1,2,0,0,0)^t,(1,0,3,0,0)^t]\subset{\bf E}^5.
Bestäm en ON-bas för det ortogonala komplementet \displaystyle W^{\perp} till \displaystyle W .
Övning 13.12
Låt \displaystyle W=[(1,1,1,1)^t,(2,0,2,0)^t]\subset{\bf E}^4 .
a) Bestäm en ON-bas för \displaystyle W .
b) Utvidga ON-basen i \displaystyle W till en ON-bas för hela \displaystyle {\bf E}^4 .
c) Låt \displaystyle \boldsymbol{u}=(0,4,4,0)^t . Bestäm ortogonala projektionerna \displaystyle P_{W}(\boldsymbol{u})=\boldsymbol{u}_{\parallel W} och \displaystyle P_{W^\perp}(\boldsymbol{u})=\boldsymbol{u}_{\parallel W^\perp} .
d) Bestäm avståndet från punkten \displaystyle (0,4,4,0) till \displaystyle W .
e) Låt \displaystyle \boldsymbol{u}=(x_1,x_2,x_3,x_4)^t . Bestäm ortogonala projektionen \displaystyle P_{W}(\boldsymbol{u}) .
Övning 13.13
Låt \displaystyle W=[(1,1,1,1)^t,(1,2,2,1)^t,(2,3,1,6)^t] .
a) Ange en ekvation för \displaystyle W .
b) Bestäm först en ON-bas för \displaystyle W och utvidga sen till en ON-bas för hela \displaystyle {\bf E}^4 .
c) Bestäm koordinaterna för \displaystyle \boldsymbol{u}=(2,2,6,2)^t i denna bas.
d) Dela upp \displaystyle \boldsymbol{u} i \displaystyle \boldsymbol{u}=\boldsymbol{u}_{\parallel W}+\boldsymbol{u}_{\parallel W^\perp} .
e) Låt \displaystyle \boldsymbol{u}=(2,2,6,2)^t och bestäm den vektor \displaystyle \boldsymbol{w}\in W som minimerar avståndet \displaystyle ||\boldsymbol{u}-\boldsymbol{w}|| , dvs ligger närmast \displaystyle \boldsymbol{u} .
f) Ange detta minimum.
Övning 13.14
Låt \displaystyle W=\{\boldsymbol{x}\in{\bf R}^4:\ x_1+2x_2-x_3+4x_4=0\} .
a) Bestäm först en ON-bas för \displaystyle W och utvidga sen till en ON-bas för hela \displaystyle {\bf E}^4 .
b) Bestäm koordinaterna för \displaystyle \boldsymbol{u}=(2,3,6,2)^t i denna bas.
c) Dela upp \displaystyle \boldsymbol{u} i \displaystyle \boldsymbol{u}=\boldsymbol{u}_{\parallel W}+\boldsymbol{u}_{\parallel W^\perp} .
d) Låt \displaystyle \boldsymbol{u}=(2,3,6,2)^t och bestäm den vektor \displaystyle \boldsymbol{w}\in W som minimerar avståndet \displaystyle ||\boldsymbol{u}-\boldsymbol{w} ||, dvs ligger närmast \displaystyle \boldsymbol{u} .
e) Ange detta minimum.
Övning 13.15
Sätt
W=[(1,1,-1,-1)^t,(1,2,-1,-2)^t,(1,3,-1,-3)^t]\subset{\bf E}^4.
a) Bestäm en ON-bas i \displaystyle W .
b) Utvidga ON-basen i a) till en ON-bas för hela \displaystyle {\bf E}^4 .
c) Dela upp \displaystyle \boldsymbol{u}=(-1,1,1,1)^t i \displaystyle \boldsymbol{u}=\boldsymbol{u}_{\parallel W}+\boldsymbol{u}_{\perp W} ,
där \displaystyle \boldsymbol{u}_{\parallel W}\in W och \displaystyle \boldsymbol{u}_{\perp W}\in W^{\perp} .
Övning 13.16
Vilken vektor i
[(1,1,1,-1)^t,(-1,1,3,-1)^t,(1,0,-1,0)^t]\subset{\bf E}^4
ligger närmast \displaystyle (1,2,3,2)^t ?
Övning 13.17
Bestäm en ON-bas för \displaystyle {\bf E}^4 , där så många som möjligt av baselementen tillhör
W=\{\boldsymbol{x}\in{\bf E}^4:\ x_1-x_2+x_3+x_4=0,\quad x_1-x_2+2x_3+x_4=0\}.

 Hämtar...
Hämtar...