Solution 5.9
From Mechanics
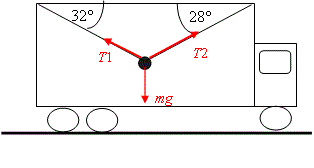
As the lorry and thus all parts of the lorry have constant velocity the forces on the load must be in equilibrium.
Resolving horisontally to the right
\displaystyle \begin{align} & T2\cos {{28}^{\circ }}-T1\cos {{32}^{\circ }}=0 \\ & \\ \end{align}
giving
\displaystyle T2=\frac{\cos {{32}^{\circ }}}{\cos {{28}^{\circ }}}T1
Resolving vertically upwards.
\displaystyle T1\cos {{58}^{\circ }}+T2\cos {{62}^{\circ }}-mg=0
Substituting for \displaystyle T2 in this equation gives an equation only containing \displaystyle T1.
\displaystyle \begin{align} & T1\cos {{58}^{\circ }}+\frac{\cos {{32}^{\circ }}}{\cos {{28}^{\circ }}}T1\cos {{62}^{\circ }}-mg=0 \\ & \\ & T1\left( \cos {{58}^{\circ }}+\frac{\cos {{32}^{\circ }}}{\cos {{28}^{\circ }}}\cos {{62}^{\circ }} \right)=mg \\ & \\ & T1\left( 0\textrm{.}53+0\textrm{.}45 \right)=40\times 9\textrm{.}8 \\ & \\ & T1=\frac{392}{0\textrm{.}98}=400\ \text{N} \\ \end{align}
and thus using \displaystyle T2=\frac{\cos {{32}^{\circ }}}{\cos {{28}^{\circ }}}T1
\displaystyle T2=\frac{0\textrm{.}848}{0\textrm{.}883}\times 400=384\ \text{N}