From Mechanics

\displaystyle \large {\underline{ {\textbf {Practice Test Paper (1 hour)}}}}

Note that the Mechanics Test counts for \displaystyle \bf 50\% of the final mechanics mark.

1. A ball is projected vertically upwards from a height of 5 metres above ground level. Its initial speed is \displaystyle 7 \ \text{ m}{{\text{s}}^{-1}} . Assume that the ball is a particle and that no resistance forces act on it as it moves.

(a) Find the maximum height of the ball above ground level.

(3 marks)

(b) Find the time that it takes the ball to reach its maximum height.

(3 marks)

2. A lift and its contents have mass 800 kg. A vertical cable is attached to the lift.

(a) Find the tension in the cable when the lift is accelerating upwards at \displaystyle 0\textrm{.}2 \text{ m}{{\text{s}}^{-2} }.

(3 marks)

(b) Find the tension in the cable when the lift is accelerating downwards at \displaystyle 0\textrm{.}2 \text{ m}{{\text{s}}^{-2} }.

(3 marks)

(c) Write down the tension in the cable when the lift is travelling at a constant speed.

(1 mark)

3. A wooden block, of mass 2 kg slides on a rough horizontal surface with a deceleration of \displaystyle 1\textrm{.}8 \text{ m}{{\text{s}}^{-2} }.

(a) Draw a diagram to show the forces on the block.

(1 mark)

(b) Show that the magnitude of the friction force acting on the block is 3.6 N.

(2 marks)

(c) Calculate the magnitude of the normal reaction force acting on the block.

(2 marks)

(d) Find the coefficient of friction between the block and the surface.

(3 marks)

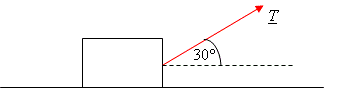
4. A heavy crate, of mass 200 kg, is pulled along a rough horizontal surface at a constant speed by a rope. The rope is at an angle of \displaystyle 30{}^\circ to the horizontal. The tension in the rope is \displaystyle T newtons. The coefficient of friction between the crate and the surface is 0.6. Model the crate as a particle.

(a) Draw a diagram to show the forces acting on the crate.

(1 mark)

(b) Show that the magnitude of the normal reaction force is \displaystyle \left( 1960-0\textrm{.}5T \right) newtons.

(3 marks)

(c) Find \displaystyle T.

(4 marks)

5. A particle is initially at the origin and has velocity \displaystyle (4\mathbf{i}+3\mathbf{j})\text{ m}{{\text{s}}^{\text{-1}}}. It moves with constant acceleration and 10 seconds later has velocity \displaystyle (5\mathbf{i}-2\mathbf{j})\text{ m}{{\text{s}}^{\text{-1}}}. The unit vectors \displaystyle \mathbf{i} and \displaystyle \mathbf{j} are directed east and north respectively.

(a) Show that the acceleration of the particle is \displaystyle (0\textrm{.}1\mathbf{i}-0\textrm{.}5\mathbf{j})\text{ m}{{\text{s}}^{\text{-2}}}.

(3 marks)

(b) Find an expression for the position vector of the particle at time t seconds.

(2 marks)

(c) Find the time when the particle is due east of the origin.

(3 marks)

(d) Find the time when the particle is moving due east.

(3 marks)

40 MARKS