5. Forces and equilibrium
From Mechanics
| Theory | Exercises | Video |
Key Points
The sum of the forces acting on a particle is called the resultant.
If the resultant of the forces acting on a particle is zero we say that these forces are in equilibrium.
The forces acting on a particle at rest or moving with constant velocity are in equilibrium.
In practical terms this means, for forces in equilibrium the sum of the components of the forces in any direction must be zero.
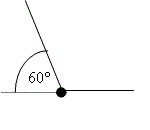
The diagram shows an object, of mass 300 kg, that is at rest and is supported by two cables. Find the tension in each cable.
Solution
The diagram shows the forces acting on the object.
Resolving horizontally or using the horizontal components of the forces:
\displaystyle \begin{align} & {{T}_{1}}\cos 60{}^\circ ={{T}_{2}}\cos 60{}^\circ \\ & {{T}_{1}}={{T}_{2}} \end{align}
Resolving vertically gives;
\displaystyle {{T}_{1}}\sin 60{}^\circ +{{T}_{2}}\sin 60{}^\circ =2940 \ \text{N}
Now solving the equations by substituting \displaystyle {{T}_{1}}={{T}_{2}}
gives:
\displaystyle \begin{align} & {{T}_{1}}\sin 60{}^\circ +{{T}_{2}}\sin 60{}^\circ =2940 \\ & 2{{T}_{1}}\sin 60{}^\circ =2940 \\ & {{T}_{1}}=\frac{2940}{2\sin 60{}^\circ }=1700\text{ N (to 3sf)} \\ \end{align}
And also \displaystyle {{T}_{2}}=1700\text{ N (to 3 sf)}.
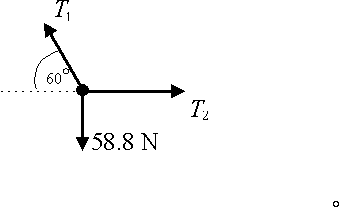
A particle of mass 6 kg is suspended by two strings as shown in the diagram. Note that one string is horizontal. Find the tension in each string.
Solution
The diagram shows the forces acting on the particle.
Resolving vertically:
\displaystyle \begin{align} & {{T}_{1}}\sin 60{}^\circ =58\textrm{.}8 \ \text{N}\\ & {{T}_{1}}=\frac{58\textrm{.}8}{\sin 60{}^\circ }=67\textrm{.}9\text{ N (to 3 sf)} \\ \end{align}
Resolving horizontally:
\displaystyle \begin{align} & {{T}_{1}}\cos 60{}^\circ ={{T}_{2}} \\ & {{T}_{2}}=\frac{58\textrm{.}8}{\sin 60{}^\circ }\cos 60{}^\circ =33\textrm{.}9\text{ N (to 3sf)} \\ \end{align}
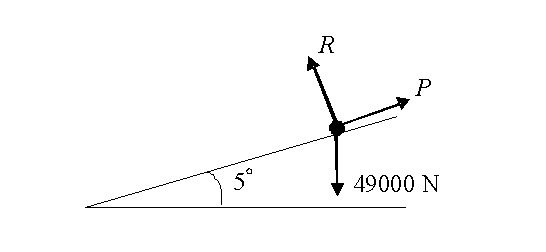
A lorry of mass 5000 kg drives up a slope inclined at \displaystyle {{5}^{\circ }} to the horizontal. The lorry moves in a straight line and at a constant speed. Assume that no resistance forces act on the lorry. Find the magnitude of the normal reaction force and force that acts on the lorry in its direction of motion.
Solution
Model the lorry as a particle.
The diagram shows the forces acting on the lorry.
Resolving perpendicular to the slope gives:
\displaystyle R=49000\cos 5{}^\circ =48800\text{ N (to 3 sf)}
Resolving parallel to the slope gives:
\displaystyle P=49000\sin 5{}^\circ =4270\text{ N (to 3sf)}
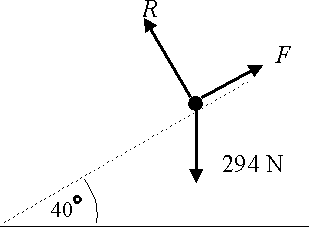
A child, of mass 30 kg, slides down a slide at a constant speed. Assume that there is no air resistance acting on the child. The slide makes an angle of \displaystyle {{40}^{\circ }} with the horizontal. Find the magnitude of the friction force on the child and the coefficient of friction.
Solution
Model the child as a particle.
The diagram shows the forces acting on the child.
Resolving parallel to the slope gives.
\displaystyle F=294\sin 40{}^\circ =189\text{ N (to 3sf)}
Resolving perpendicular to the slope gives:
\displaystyle R=294\cos 40{}^\circ \ \text{N}
As the child is sliding \displaystyle F=\mu R so that we can determine \displaystyle \mu .
\displaystyle \begin{align} & 294\sin 40{}^\circ =\mu \times 294\cos 40{}^\circ \\ & \mu =\frac{294\sin 40{}^\circ }{294\cos 40{}^\circ }=\tan 40{}^\circ =0\textrm{.}839\text{ (to 3 sf)} \\ \end{align}
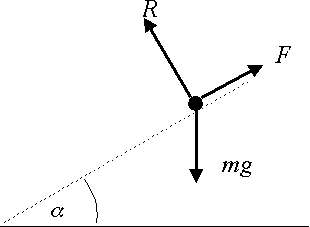
If a particle of mass \displaystyle m is at rest on a slope at an angle \displaystyle \alpha above the horizontal, then :
\displaystyle F=mg\sin \alpha
\displaystyle R=mg\cos \alpha
Then using \displaystyle F\le \mu R gives:
\displaystyle \begin{align} & mg\sin \alpha \le \mu mg\cos \alpha \\ & \mu \ge \frac{\sin \alpha }{\cos \alpha } \\ & \mu \ge \tan \alpha \\ \end{align}
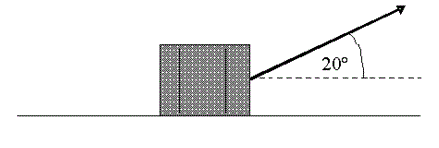
A crate of mass 200 kg is on a horizontal surface. The coefficient of friction between the crate and the surface is 0.4. The crate is pulled by a rope, as shown in the diagram, so that the crate moves at a constant speed in a straight line. Find the tension in the rope.
Solution
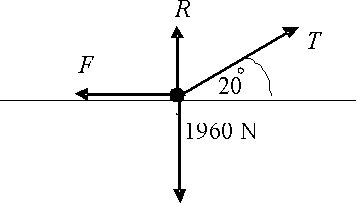
The diagram shows the forces acting on the crate.
Resolving horizontally:
\displaystyle F=T\cos 20{}^\circ \ \text{N}
Resolving vertically:
\displaystyle R+T\sin 20{}^\circ =1960
or
\displaystyle R=1960-T\sin 20{}^\circ \ \text{N}
As the crate is sliding we can use \displaystyle F=\mu R, which gives:
\displaystyle F=0\textrm{.}4R
Using this equation with the horizontal and vertical equations gives:
\displaystyle \begin{align} & T\cos 20{}^\circ =0\textrm{.}4\left( 1960-T\sin 20{}^\circ \right) \\ & T\cos 20{}^\circ =784-T\times 0\textrm{.}4\sin 20{}^\circ \\ & T\cos 20{}^\circ +T\times 0\textrm{.}4\sin 20{}^\circ =784 \\ & T\left( \cos 20{}^\circ +0\textrm{.}4\sin 20{}^\circ \right)=784 \\ & T=\frac{784}{\cos 20{}^\circ +0\textrm{.}4\sin 20{}^\circ }=728\text{ N (to 3sf)} \\ \end{align}