2. Introduction to force and gravity
From Mechanics
| Theory | Exercises | Video |
Key Points
Newton's First Law
A particle will move with a constant velocity or remain at rest if the resultant force on the particle is zero.
Equilibrium
If the resultant force on a particle is zero, then the forces acting on the particle are said to be in equilibrium.
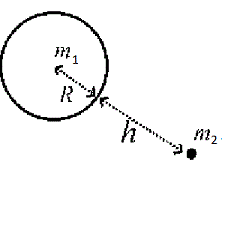
The Universal Law of Gravitation
| \displaystyle F=\frac{Gm_{1}m_{2}}{{d}^{\ 2}}
\displaystyle G=6\textrm{.}67\times 10^{-11}\text{ kg}^{\text{-1}}\text{m}^{\text{3}}\text{s}^{\text{-2}} |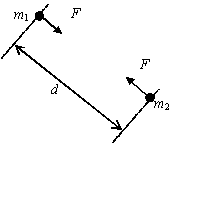 
|
Gravitational force from an heavenly body
| For a particle in the neighbourhood of a planet, moon or star the distance \displaystyle d is measured from the centre to the particle.
Thus \displaystyle d=R+h, where \displaystyle h is distance to the surface. | 
|
Gravity on Earth
The force of gravity is often called the weight.
\displaystyle \begin{align} & F=mg \\ & g=9\textrm{.}8\text{ ms}^{\text{-2}} \\ \end{align}
Data
Radius of Earth is \displaystyle \text{6}\textrm{.}\text{37}\times \text{1}0^{\text{6}}\text{ } metres
Mass of Earth is \displaystyle \text{5}\textrm{.}\text{98}\times \text{1}0^{\text{24}}\text{ } kg
Describe whether or not the forces acting on the following objects are in equilibrium:
a) A passenger in a train that travels at a constant speed.
b) A hot air balloon rising at a constant rate.
c) A stone dropped into a very deep well full of water.
Solution
a) Yes, if it is travelling in a straight line.
b) Yes, if it is travelling in a straight line.
c) Yes, if it reaches a terminal velocity, so that it is travelling in a straight line at a constant speed.
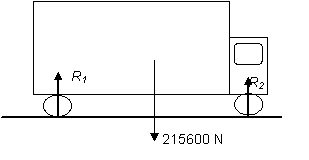
Find the magnitude of the force of gravity (weight) acting on a lorry of mass 22 tonnes.
Solution
This is calculated using the fact that the weight is given by \displaystyle mg.
\displaystyle \begin{align} & mg=22000\times 9\textrm{.}8 \\ & =215600\text{ N} \end{align}
The diagram shows the lorry and its weight.
Note that reaction forces also act upwards on each wheel.
\displaystyle {{R}_{1}}+{{R}_{2}}+{{R}_{3}}+{{R}_{4}}=215600\ \text{N}
A box of mass 30 kg is at rest on a table.
a) Calculate the weight of the box.
b) State the magnitude of the upward force that the table exerts on the box.
Solution
a)
\displaystyle \begin{align} & W=30\times 9\textrm{.}8 \\ & =294\text{ N} \end{align}
b) An upward force of 294 N must act for the box to remain in equilibrium.
A satellite, of mass 400 kg, is at a height of 12 km above the surface of the earth. Find the magnitude of the gravitational attraction on the satellite.
Data: \displaystyle G=6\textrm{.}67\times {{10}^{-11}} \displaystyle \text{k}{{\text{g}}^{-\text{1}}}{{\text{m}}^{\text{3}}}{{\text{s}}^{-\text{2}}}
Radius of earth \displaystyle =6\textrm{.}37\times {{10}^{6}} \text{m}
Mass of earth \displaystyle =5\textrm{.}98\times {{10}^{24}} \text{kg}
Solution
\displaystyle \begin{align} & \frac{G{{m}_{1}}{{m}_{2}}}{{{d}^{\ {2}}}}=\frac{6\textrm{.}67\times {{10}^{-11}}\times 400\times 5\textrm{.}98\times {{10}^{24}}}{{{\left( 6\textrm{.}37\times {{10}^{6}}+12000 \right)}^{2}}} \\ & =3917\text{ N} \end{align}
The sun has mass \displaystyle 1\textrm{.}99\times {{10}^{30}} \text{kg} . The mean distance of the earth from the sun is approximately \displaystyle 1\textrm{.}5\times {{10}^{11}} \text{m} .
(a) Calculate the force that the sun exerts on the earth.
(b) State the force that the earth exerts on the sun.
(c) Explain why this force varies.
Solution
(a)
\displaystyle \begin{align} & \frac{G{{m}_{1}}{{m}_{2}}}{{{d}^{\ 2}}}=\frac{6\textrm{.}67\times {{10}^{-11}}\times 1\textrm{.}99\times {{10}^{30}}\times 5\textrm{.}98\times {{10}^{24}}}{{{\left( 1\textrm{.}5\times {{10}^{11}} \right)}^{2}}} \\ & =3\textrm{.}53\times {{10}^{22}}\text{ N} \end{align}
(b) \displaystyle 3\textrm{.}53\times {{10}^{22}}\text{ N}
(c) The distance between the earth and the sun varies.
