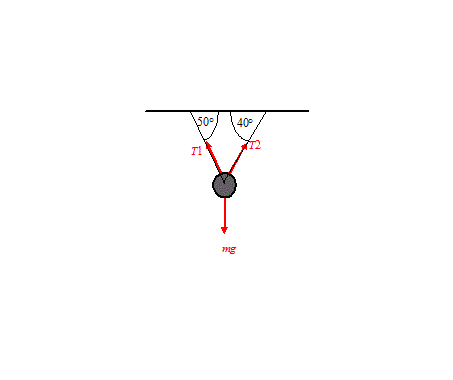
Solution 5.8
From Mechanics
Resolving horisontally to the right
\displaystyle \begin{align} & T2\cos {{40}^{\circ }}-T1\cos {{50}^{\circ }}=0 \\ & \\ \end{align}
giving
\displaystyle T2=\frac{\cos {{50}^{\circ }}}{\cos {{40}^{\circ }}}T1
Resolving vertically upwards.
\displaystyle T1\cos {{40}^{\circ }}+T2\cos {{50}^{\circ }}-mg=0
Substituting for \displaystyle T2 in this equation gives an equation only containing \displaystyle T1.
\displaystyle \begin{align} & T1\cos {{40}^{\circ }}+\frac{\cos {{50}^{\circ }}}{\cos {{40}^{\circ }}}T1\cos {{50}^{\circ }}-mg=0 \\ & \\ & T1\left( \cos {{40}^{\circ }}+\frac{{{\cos }^{2}}{{50}^{\circ }}}{\cos {{40}^{\circ }}} \right)=mg \\ & \\ & T1\left( 0\textrm{.}766+0\textrm{.}539 \right)=50\times 9\textrm{.}8 \\ & \\ & T1=\frac{490}{1\textrm{.}3}=375\ \text{N} \\ \end{align}
Also using
\displaystyle T2=\frac{\cos {{50}^{\circ }}}{\cos {{40}^{\circ }}}T1
\displaystyle T2=\frac{0\textrm{.}642}{0\textrm{.}766}\times 375=315\ \text{N}