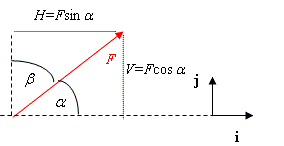From Mechanics

Using \displaystyle {{F}^{2}}={{H}^{2}}+{{V}^{2}}

and

\displaystyle \tan \alpha =\frac{V}{H}

Here

\displaystyle V=8\ \text{N} and \displaystyle H=-2\ \text{N}.

Substituting the given values

giving

Also

\displaystyle \tan \alpha =\frac{8}{-2}=-4

giving

\displaystyle \alpha =-76\textrm{.}0{}^\circ

However the force is in the second quadrant so this angle is not correct.

Another possible angle which gives the same tan is

\displaystyle \alpha =180-76\textrm{.}0=104\textrm{.}0{}^\circ

This is in the second quadrant and thus is the correct answer.