Solution 10.5
From Mechanics
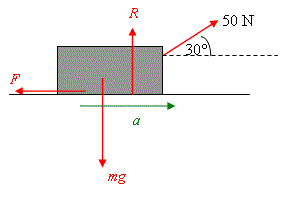
We have drawn all the forces acting on the block in the figure. The acceleration is represented by the vector \displaystyle a.
Applying Newton´s Second Law \displaystyle F=ma horisontally,
\displaystyle \begin{align} & \to :\ 50\cos {{30}^{\circ }}-F=ma \\ & \\ & F=50\cos {{30}^{\circ }}-ma=50\times 0\textrm{.}866-20\times 0.5=43\textrm{.}3-10=33\textrm{.}3\ \text{N} \\ \end{align}
We now use the friction condition \displaystyle F = \mu R, however we first need to calculate \displaystyle R.
Note that \displaystyle R is NOT equal to \displaystyle mg here as the string has a component force in the vertical direction! In fact one has,
\displaystyle \begin{align} & \uparrow :\ R+50\sin {{30}^{\circ }}-mg=0 \\ & \\ & R=mg-50\sin {{30}^{\circ }}=20\times 9\textrm{.}81-50\times \frac{1}{2}=196\textrm{.}2-25=171\textrm{.}2\ \text{N} \\ \end{align}
Using the friction equation gives
\displaystyle \begin{align}
& 33\textrm{.}3=\mu 171\textrm{.}2 \\
& \\
& \mu =\frac{33\textrm{.}3}{171\textrm{.}2}=0\textrm{.}195 \\
\end{align}