20.3 Andragradsytor
SamverkanLinalgLIU
| 20.1 | 20.2 | 20.3 | 20.4 |
Läs textavsnitt 20.3 Andragradsytor.
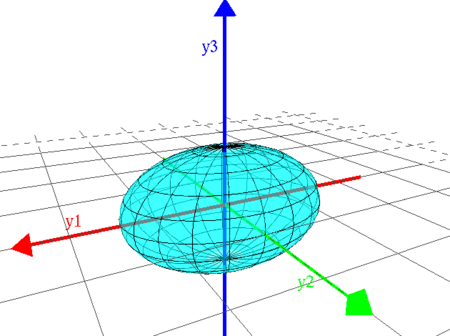
Innan Du börjar arbeta med detta moment så kan Du visualisera andragradsytor genom att klicka på bilden.
Du kan visualisera andragradsytor på allmän form genom att klicka på bilden.
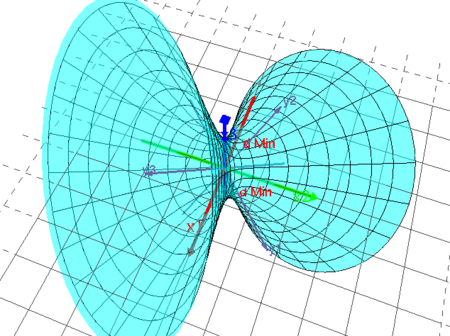
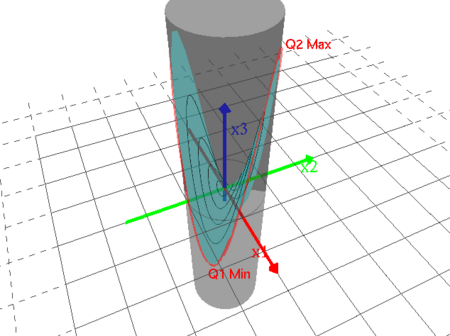
Du kan visualisera Exempel 20.7 i boken (finns också i PDF-format under länken ovan) genom att klicka på bilden.
Innehåll |
Övning 22.27
Låt \displaystyle d vara avståndet från en punkt på ytan
3x_1^2+x_2^2+x_3^2+2\sqrt3x_1x_3=1
till origo. Vilka värden kan \displaystyle d anta? I förekommande fall ange de punkter där \displaystyle d antar sitt största respektive minsta värde.
Övning 22.28
Bestäm största resp. minsta värde som den kvadratiska formen
Q=3x_2^2+3x_3^2+4x_1x_2+4x_1x_3-2x_2x_3
antar på enhetssfären \displaystyle x_1^2+x_2^2+x_3^2=1 och ange i vilka punkter extremvärdena antas.
Övning 22.29
Bestäm största och minsta värde av den kvadratiska formen
Q=x_1^2+x_2^2+x_3^2+2x_1x_2+2x_1x_3-2x_2x_3
på enhetssfären \displaystyle x_1^2+x_2^2+x_3^2=1 och ange i vilka punkter extremvärdena antas.
Övning 22.30
Betrakta den kvadratiska formen
Q(\boldsymbol{u})=Q(\underline{\boldsymbol{e}}X)=2x_1^2+2x_2^2+2x_3^2-2x_1x_2-2x_1x_3-2x_2x_3.
a) Uttryck \displaystyle Q i kanonisk bas.
b) Bestäm \displaystyle Q :s nollställen dels i den nya kanoniska basen och dels i den gamla basen.
c) Beskriv ytan
2x_1^2+2x_2^2+2x_3^2-2x_1x_2-2x_1x_3-2x_2x_3=1
och bestäm ekvationen för ett plan som skär ytan under rät vinkel.
Övning 22.31
Bestäm en gemensam punkt till ytorna
\begin{array}{rcl} 5x_1^2+8x_2^2+5x_3^2-4x_1x_2+8x_1x_3+4x_2x_3&=&9\\
x_1^2+x_2^2+x_3^2&=&1\end{array}

 Hämtar...
Hämtar...