From Mechanics

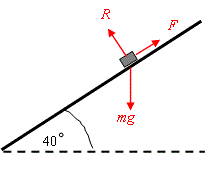
The figure shows the forces acting on the particle.

Assuming the particle has an acceleration \displaystyle a down the plane Newton´s Second Law applied down the plane gives,

\displaystyle mg\sin {{40}^{\circ }}-F=ma (equation of motion)

We need to obtain \displaystyle F.

Resolving perpendicular to the plane the sum of the forces on the particle must be zero as the particle has no motion in that direction.

\displaystyle \begin{align} & R-mg\cos {{40}^{\circ }}=0 \\ & \\ & R=mg\cos {{40}^{\circ }} \\ \end{align}

The friction condition gives

\displaystyle F=\mu R which gives

\displaystyle F=\mu mg\cos {{40}^{\circ }}

Substituting in the equation of motion above

\displaystyle mg\sin {{40}^{\circ }}-\mu mg\cos {{40}^{\circ }}=ma

We can cancel the mass \displaystyle m in this equation giving

\displaystyle g\sin {{40}^{\circ }}-\mu g\cos {{40}^{\circ }}=a or

\displaystyle \begin{align} & a=9\textrm{.}81\times 0\textrm{.}643-0\textrm{.}2\times 9\textrm{.}81\times 0.76\textrm{.}= \\ & =9\textrm{.}81\times (0\textrm{.}643-0\textrm{.}154)=9\textrm{.}81\times 0\textrm{.}489=\textrm{.}80\ \text{m}{{\text{s}}^{-2}} \\ \end{align}

Note by waiting to substitute the values of the various quantities we minimized the amount of calculation needed. Also the result is independent of the mass of the particle as we could cancel it out.