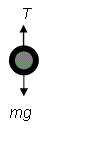Solution 3.3
From Mechanics
First consider the lower mass.
If \displaystyle T={{T}_{1}} is the tension in the lower string then
\displaystyle mg=7\times 9\textrm{.}8=68\textrm{.}6\ \text{N}
giving
\displaystyle {{T}_{1}}=68\textrm{.}6\ \text{N}
If \displaystyle T={{T}_{2}} is the tension in the upper string then the two masses are regarded as one particle with total mass 15 kg.
Thus in this case
\displaystyle mg=15\times 9\textrm{.}8=147\ \text{N}
giving
\displaystyle {{T}_{2}}=147\ \text{N}