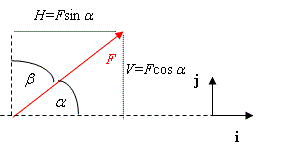Solution 4.5a
From Mechanics
(Difference between revisions)
(New page: Image:teori4.gif Using <math>{{F}^{2}}={{H}^{2}}+{{V}^{2}}</math> Substituting the given values <math>\begin{align} & {{F}^{2}}={{4}^{2}}+{ {3}^{2}} =25 \\ & F=5 \text{ N} \\ \end...) |
|||
| Line 2: | Line 2: | ||
Using <math>{{F}^{2}}={{H}^{2}}+{{V}^{2}}</math> | Using <math>{{F}^{2}}={{H}^{2}}+{{V}^{2}}</math> | ||
| + | |||
| + | and | ||
| + | |||
| + | <math>\tan \alpha =\frac{V}{H} </math> | ||
| + | |||
| + | Here | ||
| + | |||
| + | <math>V=A</math> and | ||
| + | <math>H=B</math>. | ||
Substituting the given values | Substituting the given values | ||
| + | |||
<math>\begin{align} | <math>\begin{align} | ||
| - | & {{F}^{2}}={{4}^{2}}+{ | + | & {{F}^{2}}={{4}^{2}}+{{3}^{2}}=25 \\ |
| - | {3}^{2}} | + | & \text{giving} \\ |
| - | =25 \\ | + | & F=5\ \text{N} \\ |
| - | & F=5 \text{ N} \\ | + | |
\end{align}</math> | \end{align}</math> | ||
| - | <math>\tan \alpha =\frac{V}{H}</math> | ||
| - | + | Also | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
<math>\tan \alpha =\frac{3}{4}=0\textrm{.}75</math> | <math>\tan \alpha =\frac{3}{4}=0\textrm{.}75</math> | ||
| + | |||
giving | giving | ||
| + | |||
<math>\alpha =36\textrm{.}9{}^\circ</math> | <math>\alpha =36\textrm{.}9{}^\circ</math> | ||
Revision as of 10:35, 23 March 2010
Using \displaystyle {{F}^{2}}={{H}^{2}}+{{V}^{2}}
and
\displaystyle \tan \alpha =\frac{V}{H}
Here
\displaystyle V=A and \displaystyle H=B.
Substituting the given values
\displaystyle \begin{align}
& {{F}^{2}}={{4}^{2}}+{{3}^{2}}=25 \\
& \text{giving} \\
& F=5\ \text{N} \\
\end{align}
Also
\displaystyle \tan \alpha =\frac{3}{4}=0\textrm{.}75
giving
\displaystyle \alpha =36\textrm{.}9{}^\circ