Solution 3.11c

From Mechanics

(Difference between revisions)
Jump to: navigation, search
Current revision (12:48, 21 March 2010) (edit) (undo)
 
Line 1: Line 1:
 +
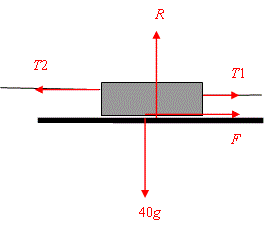
Consider the equilibrium of the block. All the forces on the block must cancel out.
 +
The following diargram shows all the forces on the block.
 +
The frictional force must point to the right, (why?).
 +
[[Image:3.11c.gif]]
[[Image:3.11c.gif]]
 +
 +
Horisontally
 +
 +
<math>\begin{align}
 +
& T2-T1-F=0 \\
 +
& F=T2-T1=245-19\textrm{.}6=225\textrm{.}4\ \text{N} \\
 +
\end{align}</math>
 +
 +
Vertically
 +
 +
<math>\begin{align}
 +
& R-40g=0\ \text{giving} \\
 +
& R=392\ \text{N} \\
 +
\end{align}</math>
 +
 +
The friction condition gives
 +
 +
<math>\begin{align}
 +
& 225\textrm{.}4\le \mu 392\ \text{or} \\
 +
& \mu \ge \frac{225\textrm{.}4}{392\ }=\frac{23}{40} \\
 +
& \\
 +
\end{align}</math>

Current revision

Consider the equilibrium of the block. All the forces on the block must cancel out. The following diargram shows all the forces on the block. The frictional force must point to the right, (why?).

Image:3.11c.gif

Horisontally

\displaystyle \begin{align} & T2-T1-F=0 \\ & F=T2-T1=245-19\textrm{.}6=225\textrm{.}4\ \text{N} \\ \end{align}

Vertically

\displaystyle \begin{align} & R-40g=0\ \text{giving} \\ & R=392\ \text{N} \\ \end{align}

The friction condition gives

\displaystyle \begin{align} & 225\textrm{.}4\le \mu 392\ \text{or} \\ & \mu \ge \frac{225\textrm{.}4}{392\ }=\frac{23}{40} \\ & \\ \end{align}

Retrieved from "http://wiki.sommarmatte.se/wikis/2009/bridgecoursemechanics/index.php/Solution_3.11c"