3. Other Forces
From Mechanics
(New page: Tensions exist in ropes and act along rope towards the centre. Tensions and thrusts exist in rods. Friction exists where rough surfaces are in contact. <math>F\le \mu R</math> The ...) |
|||
| Line 35: | Line 35: | ||
In all of the cases described above, the | In all of the cases described above, the | ||
same vertical forces act on the crate. | same vertical forces act on the crate. | ||
| + | |||
| + | [[Image:TF3.2a.GIF]] | ||
So in all of these cases R = 490, since | So in all of these cases R = 490, since | ||
Revision as of 12:48, 18 March 2009
Tensions exist in ropes and act along rope towards the centre.
Tensions and thrusts exist in rods.
Friction exists where rough surfaces are in contact.
\displaystyle F\le \mu R
The coefficient of friction is ..
The normal reaction force is R.
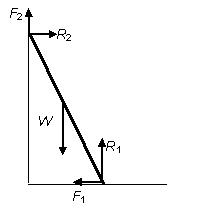
Draw a diagram to show the forces acting on a ladder leaning against a wall.
Solution
Note it has been assumed that the wall is vertical and the ground horizontal
The coefficient of friction between a crate, of mass 50 kg, and the floor is 0.7. Find the magnitude of the friction force acting on the crate if it is on a horizontal surface and; (a) no horizontal force acts on the crate, (b) a horizontal force of 80 N acts on the crate, (c) A horizontal force of 400 N acts on the crate.
Solution
In all of the cases described above, the same vertical forces act on the crate.
So in all of these cases R = 490, since the vertical forces are in equilibrium.
Using the friction inequality gives, ` \displaystyle \begin{align} & F\le \mu R \\ & F\le 0.7\times 490 \\ & F\le 343 \\ \end{align}
So the maximum friction force in this situation is 343 N.
(a) If no horizontal force acts on the crate there will be no friction force.
(b) If a horizontal force of 80 N acts on the crate the forces will be as shown in the diagram.
In this case F will take the value that is needed to produce equilibrium, provided that it is less than 343 N.
In this case F = 80 N, as this produces equilibrium, but is less than the maximum of 343 N.
(c) The forces are now as shown in the diagram.
A force of 400 N would be needed to produce equilibrium. As this is greater than the maximum friction, F takes its maximum value of 343 N.
F = 343 N
In this case there is a resultant force of 57 N to the right.
The diagram shows a block that is at rest on a horizontal plane. Two light ropes, attached to the block pass over pulleys and are also attached to masses as shown in the diagram. Find the tension in each rope and the friction between the block and the plane and an inequality that the coefficient of friction must satisfy.
Solution
Considering the 8 kg mass, which is in equilibrium gives,
\displaystyle {{T}_{1}}=78.4\text{ N}
Considering the 12 kg mass, which is also in equilibrium gives,
\displaystyle {{T}_{2}}=117.6\text{ N}
Now consider the block on the plane, which is also in equilibrium.
Vertically:
\displaystyle R=196
Horizontally
\displaystyle \begin{align} & {{T}_{1}}+F={{T}_{2}} \\ & F={{T}_{2}}-{{T}_{1}} \\ \end{align}
Using the values for the two tensions gives,
\displaystyle \begin{align} & F=117.6-78.4 \\ & =39.2 \end{align}
Using the friction inequlity
\displaystyle F\le \mu R
gives,
\displaystyle \begin{align} & 39.2\le \mu \times 196 \\ & \mu \ge \frac{39.2}{196}=0.2 \\ \end{align}
Two boxes are placed on top of each other on a horizontal surface as shown in the diagram. The top box has mass 5 kg and the lower box has mass 10 kg. Draw diagrams to show the forces acting on each box and calculate the magnitude of each of these forces.
Solution
\displaystyle {{R}_{1}}={{W}_{1}}
\displaystyle \begin{align} & {{R}_{2}}={{R}_{1}}+{{W}_{2}} \\ & ={{W}_{1}}+{{W}_{2}} \end{align}
A crate has mass 250 kg and rests on a horizontal surface. The coefficient of friction between the crate and the surface is 0.6. A horizontal force of magnitude P N is applied to the crate. What is the resultant force on the box if: (a) P = 1200 N (b) P = 1700 N
Solution
In this case \displaystyle R=W=250\times 9.8=2450\text{ N} .
Hence using \displaystyle F\le \mu R gives,
\displaystyle \begin{align} & F\le 0.6\times 2450 \\ & F\le 1470\text{ N} \\ \end{align}
(a) In this case
\displaystyle F=1200
and the resultant force is zero.
(b) In this case \displaystyle F=1470 and the resultant force is 230 N in the direction of P.