From Mechanics

Revision as of 11:02, 17 September 2010 (edit) Ian (Talk | contribs) (New page: First find the angle, <math>\alpha </math>, between the impulse and the initial velocity. <math>\begin{align} & \tan \alpha =\frac{12}{24} \\ &\\ & \alpha =26\textrm{.}6{}^\circ \e...) ← Previous diff		Current revision (11:52, 17 September 2010) (edit) (undo) Ian (Talk | contribs)
Line 1:		Line 1:
		+	[[Image:15.7temp.gif]]
		+
	First find the angle,		First find the angle,
	<math>\alpha </math>, between		<math>\alpha </math>, between

---

Current revision

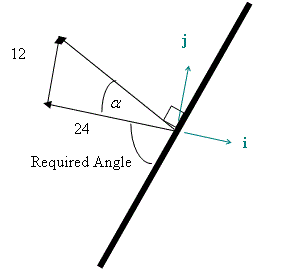
First find the angle, \displaystyle \alpha , between the impulse and the initial velocity.

\displaystyle \begin{align} & \tan \alpha =\frac{12}{24} \\ &\\ & \alpha =26\textrm{.}6{}^\circ \end{align}

Then subtract this from \displaystyle {{90}^{\circ }} to get the angle between the initial velocity and the wall.

\displaystyle \text{Angle =}90-26\textrm{.}6={{63\textrm{.}4}^{\circ }}