Solution 14.5a
From Mechanics
Ian (Talk | contribs)
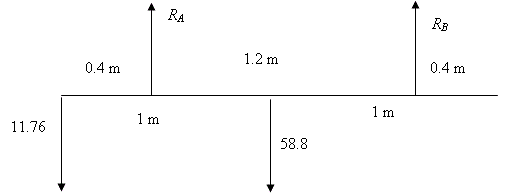
(New page: The diagram shows the forces acting on the beam Image:14.5a.gif Taking moments about the left hand support: <math>\begin{align} & 1\textrm{.}2\times {{R}_{B}}+0\textrm{.}4\time...)
Next diff →
Current revision
The diagram shows the forces acting on the beam
Taking moments about the left hand support:
\displaystyle \begin{align} & 1\textrm{.}2\times {{R}_{B}}+0\textrm{.}4\times 11\textrm{.}76=0\textrm{.}6\times 58\textrm{.}8 \\ & {{R}_{B}}=\frac{0.6\times 58\textrm{.}8-0\textrm{.}4\times 11\textrm{.}76}{1\textrm{.}2}=25\textrm{.}48\text{ N} \\ \end{align}
Taking moments about the right hand support:
\displaystyle \begin{align} & 1\textrm{.}2\times {{R}_{A}}=1\textrm{.}6\times 11\textrm{.}76+0\textrm{.}8\times 58\textrm{.}8 \\ & {{R}_{A}}=\frac{1\textrm{.}6\times 11\textrm{.}76+0\textrm{.}6\times 58\textrm{.}8}{1\textrm{.}2}=45\textrm{.}08\text{ N} \\ \end{align}
Or
\displaystyle \begin{align} & {{R}_{A}}+25\textrm{.}48=11\textrm{.}76+58\textrm{.}8 \\ & {{R}_{A}}=11\textrm{.}76+58\textrm{.}8-25\textrm{.}48=45\textrm{.}08\text{ N} \\ \end{align}