Solution 9.6b
From Mechanics
(Difference between revisions)
(New page: Image:9.6.gif) |
|||
| Line 1: | Line 1: | ||
[[Image:9.6.gif]] | [[Image:9.6.gif]] | ||
| + | |||
| + | From part a) <math>\ T=1380 \text{ N}</math>. | ||
| + | |||
| + | Resolving perpendicular to the hill, | ||
| + | |||
| + | <math>\begin{align} | ||
| + | & R+T\sin {{7}^{\circ }}-mg\cos {{5}^{\circ }}=0 \\ | ||
| + | & \\ | ||
| + | & R=mg\cos {{5}^{\circ }}-T\sin {{7}^{\circ }}=1600\times 9\textrm{.}81\times 0\textrm{.}996-1380\times 0\textrm{.}122= \\ | ||
| + | & =15633-168=15465\simeq 15500\ \text{N} \\ | ||
| + | \end{align}</math> | ||
Current revision
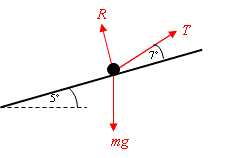
From part a) \displaystyle \ T=1380 \text{ N}.
Resolving perpendicular to the hill,
\displaystyle \begin{align} & R+T\sin {{7}^{\circ }}-mg\cos {{5}^{\circ }}=0 \\ & \\ & R=mg\cos {{5}^{\circ }}-T\sin {{7}^{\circ }}=1600\times 9\textrm{.}81\times 0\textrm{.}996-1380\times 0\textrm{.}122= \\ & =15633-168=15465\simeq 15500\ \text{N} \\ \end{align}