From Mechanics

Revision as of 13:18, 12 October 2010 (edit) Ian (Talk | contribs) (New page: We start by converting the speed to SI units. <math>60\text{ km/h }=\frac{60\times 1000}{60\times 60}=\frac{50}{3}=\text{16}\textrm{.}\text{7 m}{{\text{s}}^{\text{-1}}}</math> The diagra...) ← Previous diff		Current revision (13:20, 12 October 2010) (edit) (undo) Ian (Talk | contribs)
Line 14:		Line 14:
	& F\le \mu R \\		& F\le \mu R \\
	& 5556\le \mu \times 9800 \\		& 5556\le \mu \times 9800 \\
		+	& \\
	& \mu \ge \frac{5556}{9800} \\		& \mu \ge \frac{5556}{9800} \\
-	& \mu \ge 0.567 \\	+	& \mu \ge 0\textrm{.}567 \\
	\end{align}</math>		\end{align}</math>

---

Current revision

We start by converting the speed to SI units.

\displaystyle 60\text{ km/h }=\frac{60\times 1000}{60\times 60}=\frac{50}{3}=\text{16}\textrm{.}\text{7 m}{{\text{s}}^{\text{-1}}}

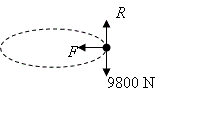
The diagram shows the forces on the car.

\displaystyle F=m\frac{{{v}^{2}}}{r}=1000\times \frac{{{\left( \frac{50}{3} \right)}^{2}}}{50}=5556\text{ N}

\displaystyle R=mg=9800

\displaystyle \begin{align} & F\le \mu R \\ & 5556\le \mu \times 9800 \\ & \\ & \mu \ge \frac{5556}{9800} \\ & \mu \ge 0\textrm{.}567 \\ \end{align}