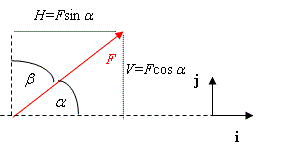4. Forces and vectors
From Mechanics
| (10 intermediate revisions not shown.) | |||
| Line 2: | Line 2: | ||
{| border="0" cellspacing="0" cellpadding="0" height="30" width="100%" | {| border="0" cellspacing="0" cellpadding="0" height="30" width="100%" | ||
| style="border-bottom:1px solid #797979" width="5px" | | | style="border-bottom:1px solid #797979" width="5px" | | ||
| - | {{Selected tab|[[ | + | {{Selected tab|[[4. Forces and vectors|Theory]]}} |
| - | {{Not selected tab|[[ | + | {{Not selected tab|[[4. Exercises|Exercises]]}} |
| style="border-bottom:1px solid #797979" width="100%"| | | style="border-bottom:1px solid #797979" width="100%"| | ||
|} | |} | ||
| + | |||
| + | == '''Key Points''' == | ||
| + | |||
| + | The force <math>\mathbf{F}</math> can be resolved into components as follows. | ||
<math>\begin{align} | <math>\begin{align} | ||
| Line 13: | Line 17: | ||
\end{align}</math> | \end{align}</math> | ||
| + | [[Image:teori4.gif]] | ||
| - | + | <math>F</math> is the magnitude of the force. | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
<math>F\cos \alpha </math> | <math>F\cos \alpha </math> | ||
| Line 25: | Line 26: | ||
<math>F\cos \alpha </math> | <math>F\cos \alpha </math> | ||
is called the horizontal component of the force. | is called the horizontal component of the force. | ||
| - | |||
<math>F\sin \alpha </math> | <math>F\sin \alpha </math> | ||
| Line 31: | Line 31: | ||
<math>F\sin \alpha </math> | <math>F\sin \alpha </math> | ||
is called the vertical component of the force. | is called the vertical component of the force. | ||
| + | |||
| + | If <math>H</math> is the horizontal component of the force and | ||
| + | |||
| + | <math>V</math> is the verical component of the force | ||
| + | |||
| + | The figure shows | ||
| + | |||
| + | <math>{{F}^{2}}={{H}^{2}}+{{V}^{2}}</math> | ||
| + | |||
| + | and also how to calculate the angles <math>\alpha</math> and <math>\beta</math>, for example, | ||
| + | |||
| + | <math>\tan \alpha =\frac{V}{H}</math> if <math>H</math> and <math>V</math> are known. | ||
| + | |||
| + | '''Note''' | ||
| + | |||
| + | This equation has infinitely many solutions as if | ||
| + | <math>\alpha </math> | ||
| + | is a solution then | ||
| + | <math>\alpha \pm 180</math> | ||
| + | is also a solution. | ||
| + | |||
| + | In this course it is assumed the solution chosen is between | ||
| + | <math>-180<\alpha \le 180</math>. | ||
| + | Then this equation always has two solutions for | ||
| + | <math>\alpha </math>, | ||
| + | giving two distinct directions. The solution in the quadrant that corresponds to the direction of the vector must be chosen. | ||
| + | |||
| + | |||
| + | [[Image:teori4a.gif]] | ||
| + | |||
'''[[Example 4.1]]''' | '''[[Example 4.1]]''' | ||
| Line 36: | Line 66: | ||
Express each of the forces given below in the form a<math>\mathbf{i}</math> + b<math>\mathbf{j}</math>. | Express each of the forces given below in the form a<math>\mathbf{i}</math> + b<math>\mathbf{j}</math>. | ||
| - | + | a) | |
[[Image:TF4.1a.GIF]] | [[Image:TF4.1a.GIF]] | ||
| - | + | b) | |
[[Image:TF4.1b.GIF]] | [[Image:TF4.1b.GIF]] | ||
| Line 46: | Line 76: | ||
'''Solution''' | '''Solution''' | ||
| - | + | a) <math>20\cos 40{}^\circ \mathbf{i}+20\sin 40{}^\circ \mathbf{j}\ \text{N}</math> | |
| - | + | ||
| - | <math>20\cos 40{}^\circ \mathbf{i}+20\sin 40{}^\circ \mathbf{j} | + | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| + | b) <math>-80\cos 30{}^\circ \mathbf{i}+80\sin 30{}^\circ \mathbf{j}\ \text{N}</math> | ||
Note the negative sign here in the first term. | Note the negative sign here in the first term. | ||
| - | |||
'''[[Example 4.2]]''' | '''[[Example 4.2]]''' | ||
| Line 66: | Line 89: | ||
[[Image:TF4.2.GIF]] | [[Image:TF4.2.GIF]] | ||
| - | |||
'''Solution''' | '''Solution''' | ||
| - | |||
| - | <math>28\cos 30{}^\circ \mathbf{i}-28\sin 30{}^\circ \mathbf{j}</math> | + | <math>28\cos 30{}^\circ \mathbf{i}-28\sin 30{}^\circ \mathbf{j}\ \text{N}</math> |
| - | + | ||
Note the negative sign in the second term. | Note the negative sign in the second term. | ||
| - | |||
'''[[Example 4.3]]''' | '''[[Example 4.3]]''' | ||
| - | |||
Express the force shown below as a vector in terms of | Express the force shown below as a vector in terms of | ||
| Line 91: | Line 109: | ||
'''Solution''' | '''Solution''' | ||
| - | + | ||
| - | + | <math>-50\cos 44{}^\circ \mathbf{i}-50\sin 44{}^\circ \mathbf{j}\ \text{N}</math> | |
| - | <math>-50\cos 44{}^\circ \mathbf{i}-50\sin 44{}^\circ \mathbf{j}</math> | + | |
| - | + | ||
Note that here both terms are negative. | Note that here both terms are negative. | ||
| Line 109: | Line 125: | ||
| - | The magnitude, | + | The magnitude, <math>F</math> , of the force is given by, |
| - | <math>F=\sqrt{{{4}^{2}}+{{8}^{2}}}=\sqrt{80}=8.94\text{ N (to 3sf)}</math> | + | <math>F=\sqrt{{{4}^{2}}+{{8}^{2}}}=\sqrt{80}=8\textrm{.}94\text{ N (to 3sf)}</math> |
The angle, <math>\theta </math>, is given by, | The angle, <math>\theta </math>, is given by, | ||
| - | <math>\theta ={{\tan }^{-1}}\left( \frac{8}{4} \right)=63.4{}^\circ </math> | + | <math>\theta ={{\tan }^{-1}}\left( \frac{8}{4} \right)=63\textrm{.}4{}^\circ </math> |
| Line 122: | Line 138: | ||
Find the magnitude and direction of the resultant of the four forces shown in the diagram. | Find the magnitude and direction of the resultant of the four forces shown in the diagram. | ||
| - | |||
[[Image:TF4.5.GIF]] | [[Image:TF4.5.GIF]] | ||
| - | |||
'''Solution''' | '''Solution''' | ||
| - | Force Vector Form | + | {| width="100%" cellspacing="10px" align="center" |
| - | 20 N | + | |align="left"| Force |
| - | <math>20\cos 50{}^\circ \mathbf{i}+20\sin 50{}^\circ \mathbf{j}</math> | + | | valign="top"|Vector Form (N) |
| - | + | |- | |
| - | 18 N | + | |20 N |
| - | <math>-18\mathbf{j}</math> | + | | valign="top"| <math>20\cos 50{}^\circ \mathbf{i}+20\sin 50{}^\circ \mathbf{j}</math> |
| - | + | |- | |
| - | 25 N | + | | 18 N |
| - | <math>-25\cos 20{}^\circ \mathbf{i}-25\sin 20{}^\circ \mathbf{j}</math> | + | |valign="top"| <math>-18\mathbf{j}</math> |
| - | + | |- | |
| - | 15 N | + | | 25 N |
| - | <math>-15\cos 30{}^\circ \mathbf{i}+15\sin 30{}^\circ \mathbf{j}</math> | + | |valign="top"|<math>-25\cos 20{}^\circ \mathbf{i}-25\sin 20{}^\circ \mathbf{j}</math> |
| - | + | |- | |
| - | + | | 15 N | |
| + | |valign="top"|<math>-15\cos 30{}^\circ \mathbf{i}+15\sin 30{}^\circ \mathbf{j}</math> | ||
| + | |} | ||
<math>\begin{align} | <math>\begin{align} | ||
| - | & \text{Resultant Force }=\text{ }\left( 20\cos 50{}^\circ -25\cos 20{}^\circ -15\cos 30{}^\circ \right)\mathbf{i}+\left( 20\sin 50{}^\circ -18-25\sin 20{}^\circ +15\sin 30{}^\circ \right)\mathbf{j} | + | & \text{Resultant Force }=\text{ }\left( 20\cos 50{}^\circ -25\cos 20{}^\circ -15\cos 30{}^\circ \right)\mathbf{i}+ \\ |
| - | + | & \left( 20\sin 50{}^\circ -18-25\sin 20{}^\circ +15\sin 30{}^\circ \right)\mathbf{j}=-23.627\mathbf{i}-3.730\mathbf{j} \text{ N} | |
\end{align}</math> | \end{align}</math> | ||
| - | |||
The magnitude is given by: | The magnitude is given by: | ||
| - | + | ||
| - | + | <math>\sqrt{{{23\textrm{.}627}^{2}}+{{3\textrm{.}730}^{2}}}=23\textrm{.}9\text{ N (to 3sf)}</math> | |
| - | <math>\sqrt{{{23.627}^{2}}+{{3.730}^{2}}}=23.9\text{ N (to 3sf)}</math> | + | |
| - | + | ||
| - | + | ||
The angle <math>\theta </math> can be found using tan. | The angle <math>\theta </math> can be found using tan. | ||
| - | + | ||
| - | + | ||
<math>\begin{align} | <math>\begin{align} | ||
| - | & \tan \theta =\frac{3.730}{23.627} \\ | + | & \tan \theta =\frac{3\textrm{.}730}{23\textrm{.}627} \\ |
| - | & \theta =9.0{}^\circ | + | & \theta =9\textrm{.}0{}^\circ |
\end{align}</math> | \end{align}</math> | ||
| - | |||
[[Image:TF4.5a.GIF]] | [[Image:TF4.5a.GIF]] | ||
Current revision
| Theory | Exercises |
Key Points
The force \displaystyle \mathbf{F} can be resolved into components as follows.
\displaystyle \begin{align} & \mathbf{F}=F\cos \alpha \mathbf{i}+F\cos (90-\alpha )\mathbf{j} \\ & =F\cos \alpha \mathbf{i}+F\sin \alpha \mathbf{j} \end{align}
\displaystyle F is the magnitude of the force.
\displaystyle F\cos \alpha is one component of the force. If \displaystyle \mathbf{i} is horizontal, \displaystyle F\cos \alpha is called the horizontal component of the force.
\displaystyle F\sin \alpha is another component of the force. If \displaystyle \mathbf{j} is vertical, \displaystyle F\sin \alpha is called the vertical component of the force.
If \displaystyle H is the horizontal component of the force and
\displaystyle V is the verical component of the force
The figure shows
\displaystyle {{F}^{2}}={{H}^{2}}+{{V}^{2}}
and also how to calculate the angles \displaystyle \alpha and \displaystyle \beta, for example,
\displaystyle \tan \alpha =\frac{V}{H} if \displaystyle H and \displaystyle V are known.
Note
This equation has infinitely many solutions as if \displaystyle \alpha is a solution then \displaystyle \alpha \pm 180 is also a solution.
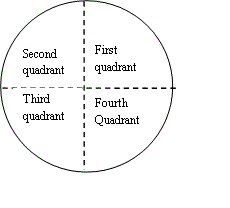
In this course it is assumed the solution chosen is between \displaystyle -180<\alpha \le 180. Then this equation always has two solutions for \displaystyle \alpha , giving two distinct directions. The solution in the quadrant that corresponds to the direction of the vector must be chosen.
Express each of the forces given below in the form a\displaystyle \mathbf{i} + b\displaystyle \mathbf{j}.
a)
b)
Solution
a) \displaystyle 20\cos 40{}^\circ \mathbf{i}+20\sin 40{}^\circ \mathbf{j}\ \text{N}
b) \displaystyle -80\cos 30{}^\circ \mathbf{i}+80\sin 30{}^\circ \mathbf{j}\ \text{N}
Note the negative sign here in the first term.
Express the force shown below as a vector in terms of \displaystyle \mathbf{i} and \displaystyle \mathbf{j}.
Solution
\displaystyle 28\cos 30{}^\circ \mathbf{i}-28\sin 30{}^\circ \mathbf{j}\ \text{N}
Note the negative sign in the second term.
Express the force shown below as a vector in terms of \displaystyle \mathbf{i} and \displaystyle \mathbf{j}
Solution
\displaystyle -50\cos 44{}^\circ \mathbf{i}-50\sin 44{}^\circ \mathbf{j}\ \text{N}
Note that here both terms are negative.
Find the magnitude of the force (4\displaystyle \mathbf{i} - 8\displaystyle \mathbf{j}) N. Draw a diagram to show the direction of this force.
Solution
The magnitude, \displaystyle F , of the force is given by,
\displaystyle F=\sqrt{{{4}^{2}}+{{8}^{2}}}=\sqrt{80}=8\textrm{.}94\text{ N (to 3sf)}
The angle, \displaystyle \theta , is given by,
\displaystyle \theta ={{\tan }^{-1}}\left( \frac{8}{4} \right)=63\textrm{.}4{}^\circ
Find the magnitude and direction of the resultant of the four forces shown in the diagram.
Solution
| Force | Vector Form (N) |
| 20 N | \displaystyle 20\cos 50{}^\circ \mathbf{i}+20\sin 50{}^\circ \mathbf{j} |
| 18 N | \displaystyle -18\mathbf{j} |
| 25 N | \displaystyle -25\cos 20{}^\circ \mathbf{i}-25\sin 20{}^\circ \mathbf{j} |
| 15 N | \displaystyle -15\cos 30{}^\circ \mathbf{i}+15\sin 30{}^\circ \mathbf{j} |
\displaystyle \begin{align} & \text{Resultant Force }=\text{ }\left( 20\cos 50{}^\circ -25\cos 20{}^\circ -15\cos 30{}^\circ \right)\mathbf{i}+ \\ & \left( 20\sin 50{}^\circ -18-25\sin 20{}^\circ +15\sin 30{}^\circ \right)\mathbf{j}=-23.627\mathbf{i}-3.730\mathbf{j} \text{ N} \end{align}
The magnitude is given by:
\displaystyle \sqrt{{{23\textrm{.}627}^{2}}+{{3\textrm{.}730}^{2}}}=23\textrm{.}9\text{ N (to 3sf)}
The angle \displaystyle \theta can be found using tan.
\displaystyle \begin{align} & \tan \theta =\frac{3\textrm{.}730}{23\textrm{.}627} \\ & \theta =9\textrm{.}0{}^\circ \end{align}