From Mechanics

Revision as of 15:58, 23 March 2010 (edit) Ian (Talk | contribs) (New page: Resultant force <math>=80\textrm{.}9\mathbf{i}-11\textrm{.}3\mathbf{j}\ \text{N}</math> Thus <math>\tan \alpha =\frac{-11\textrm{.}3}{80.9}=-0\textrm{.}14</math> giving <math>\alpha =-...) ← Previous diff		Current revision (16:13, 4 February 2011) (edit) (undo) Ian (Talk | contribs)
(One intermediate revision not shown.)
Line 4:		Line 4:
	Thus		Thus
-	<math>\tan \alpha =\frac{-11\textrm{.}3}{80.9}=-0\textrm{.}14</math>	+	<math>\tan \alpha =\frac{-11\textrm{.}3}{80\textrm{.}9}=-0\textrm{.}14</math>
	giving		giving
Line 11:		Line 11:
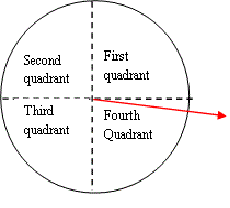
	As the vector is in the fourth quadrant		As the vector is in the fourth quadrant
		+
		+	[[Image:4.6c.gif]]

---

Current revision

Resultant force \displaystyle =80\textrm{.}9\mathbf{i}-11\textrm{.}3\mathbf{j}\ \text{N}

Thus

\displaystyle \tan \alpha =\frac{-11\textrm{.}3}{80\textrm{.}9}=-0\textrm{.}14

giving

\displaystyle \alpha =-8\textrm{.}0{}^\circ

As the vector is in the fourth quadrant