Practice Test Paper 1

From Mechanics

(Difference between revisions)
Jump to: navigation, search
Current revision (14:31, 12 January 2011) (edit) (undo)
 
(6 intermediate revisions not shown.)
Line 1: Line 1:
<math>\large {\underline{ {\textbf {Practice Test Paper (1 hour)}}}}</math>
<math>\large {\underline{ {\textbf {Practice Test Paper (1 hour)}}}}</math>
-
Note that the Mechanics Test counts for <math>50\%</math> of the final mechanics mark.
+
 
 +
'''Note that the Mechanics Test counts for <math> \bf 50\%</math> of the final mechanics mark.'''
 +
 
1. A ball is projected vertically upwards from a height of 5 metres above ground level. Its initial speed is <math>7 \ \text{ m}{{\text{s}}^{-1}} </math>. Assume that the ball is a particle and that no resistance forces act on it as it moves.
1. A ball is projected vertically upwards from a height of 5 metres above ground level. Its initial speed is <math>7 \ \text{ m}{{\text{s}}^{-1}} </math>. Assume that the ball is a particle and that no resistance forces act on it as it moves.
(a) Find the maximum height of the ball above ground level.
(a) Find the maximum height of the ball above ground level.
-
(3 marks)
+
<p style="text-align: right;"> (''3 marks'')</P>
(b) Find the time that it takes the ball to reach its maximum height.
(b) Find the time that it takes the ball to reach its maximum height.
-
(3 marks)
+
<p style="text-align: right;">(''3 marks'')</P>
Line 15: Line 17:
2. A lift and its contents have mass 800 kg. A vertical cable is attached to the lift.
2. A lift and its contents have mass 800 kg. A vertical cable is attached to the lift.
-
(a) Find the tension in the cable when the lift is accelerating upwards at 0.2 ms-2.
+
(a) Find the tension in the cable when the lift is accelerating upwards at <math> 0\textrm{.}2 \text{ m}{{\text{s}}^{-2} }</math>.
-
(3 marks)
+
<p style="text-align: right;">(''3 marks'')</P>
-
(b) Find the tension in the cable when the lift is accelerating downwards at 0.2 ms-2.
+
(b) Find the tension in the cable when the lift is accelerating downwards at <math> 0\textrm{.}2 \text{ m}{{\text{s}}^{-2} }</math>.
-
(3 marks)
+
<p style="text-align: right;">(''3 marks'')</P>
(c) Write down the tension in the cable when the lift is travelling at a constant speed.
(c) Write down the tension in the cable when the lift is travelling at a constant speed.
-
(1 mark)
+
<p style="text-align: right;">(''1 mark'')</P>
-
3. A wooden block, of mass 2 kg slides on a rough horizontal surface with a deceleration of 1.8 ms-2.
+
 
 +
3. A wooden block, of mass 2 kg slides on a rough horizontal surface with a deceleration of <math> 1\textrm{.}8 \text{ m}{{\text{s}}^{-2} }</math>.
(a) Draw a diagram to show the forces on the block.
(a) Draw a diagram to show the forces on the block.
-
(1 mark)
+
<p style="text-align: right;">''(1 mark'')</P>
 +
 
(b) Show that the magnitude of the friction force acting on the block is 3.6 N.
(b) Show that the magnitude of the friction force acting on the block is 3.6 N.
-
(2 marks)
+
<p style="text-align: right;">(''2 marks'')</P>
 +
 
(c) Calculate the magnitude of the normal reaction force acting on the block.
(c) Calculate the magnitude of the normal reaction force acting on the block.
-
(2 marks)
+
<p style="text-align: right;">(''2 marks'')</P>
 +
 
(d) Find the coefficient of friction between the block and the surface.
(d) Find the coefficient of friction between the block and the surface.
-
(3 marks)
+
<p style="text-align: right;">(''3 marks'')</P>
-
4. A heavy crate, of mass 200 kg, is pulled along a rough horizontal surface at a constant speed by a rope. The rope is at an angle of 30 to the horizontal. The tension in the rope is T newtons. The coefficient of friction between the crate and the surface is 0.6. Model the crate as a particle.
+
 +
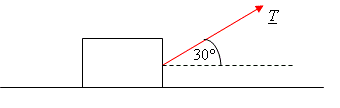
4. A heavy crate, of mass 200 kg, is pulled along a rough horizontal surface at a constant speed by a rope. The rope is at an angle of <math>30{}^\circ</math> to the horizontal. The tension in the rope is <math>T</math> newtons. The coefficient of friction between the crate and the surface is 0.6. Model the crate as a particle.
 +
[[Image:test1.4a.gif]]
 +
(a) Draw a diagram to show the forces acting on the crate.
 +
<p style="text-align: right;">(''1 mark'')</P>
 +
(b) Show that the magnitude of the normal reaction force is <math>\left( 1960-0\textrm{.}5T \right)</math> newtons.
 +
<p style="text-align: right;">(''3 marks'')</P>
 +
(c) Find <math>T</math>.
 +
<p style="text-align: right;">(''4 marks'')</P>
 +
5. A particle is initially at the origin and has velocity <math>(4\mathbf{i}+3\mathbf{j})\text{ m}{{\text{s}}^{\text{-1}}}</math>. It moves with constant acceleration and 10 seconds later has velocity <math>(5\mathbf{i}-2\mathbf{j})\text{ m}{{\text{s}}^{\text{-1}}}</math>. The unit vectors <math>\mathbf{i}</math> and <math>\mathbf{j}</math> are directed east and north respectively.
-
(a) Draw a diagram to show the forces acting on the crate.
+
(a) Show that the acceleration of the particle is <math>(0\textrm{.}1\mathbf{i}-0\textrm{.}5\mathbf{j})\text{ m}{{\text{s}}^{\text{-2}}}</math>.
-
(1 mark)
+
<p style="text-align: right;">(''3 marks'')</P>
-
(b) Show that the magnitude of the normal reaction force is newtons.
+
-
(3 marks)
+
-
(c) Find T.
+
-
(4 marks)
+
-
 
+
-
5. A particle is initially at the origin and has velocity . It moves with constant acceleration and 10 seconds later has velocity . The unit vectors i and j are directed east and north respectively.
+
-
(a) Show that the acceleration of the particle is .
+
(b) Find an expression for the position vector of the particle at time ''t'' seconds.
-
(3 marks)
+
<p style="text-align: right;">(''2 marks'')</P>
-
 
+
-
(b) Find an expression for the position vector of the particle at time t seconds.
+
-
(2 marks)
+
(c) Find the time when the particle is due east of the origin.
(c) Find the time when the particle is due east of the origin.
-
(3 marks)
+
<p style="text-align: right;">(''3 marks'')</P>
(d) Find the time when the particle is moving due east.
(d) Find the time when the particle is moving due east.
-
(3 marks)
+
<p style="text-align: right;">(''3 marks'')</P>
 +
 
 +
 
-
40 MARKS
+
'''40 MARKS'''

Current revision

\displaystyle \large {\underline{ {\textbf {Practice Test Paper (1 hour)}}}}


Note that the Mechanics Test counts for \displaystyle \bf 50\% of the final mechanics mark.


1. A ball is projected vertically upwards from a height of 5 metres above ground level. Its initial speed is \displaystyle 7 \ \text{ m}{{\text{s}}^{-1}} . Assume that the ball is a particle and that no resistance forces act on it as it moves.

(a) Find the maximum height of the ball above ground level.

(3 marks)

(b) Find the time that it takes the ball to reach its maximum height.

(3 marks)


2. A lift and its contents have mass 800 kg. A vertical cable is attached to the lift.

(a) Find the tension in the cable when the lift is accelerating upwards at \displaystyle 0\textrm{.}2 \text{ m}{{\text{s}}^{-2} }.

(3 marks)

(b) Find the tension in the cable when the lift is accelerating downwards at \displaystyle 0\textrm{.}2 \text{ m}{{\text{s}}^{-2} }.

(3 marks)

(c) Write down the tension in the cable when the lift is travelling at a constant speed.

(1 mark)


3. A wooden block, of mass 2 kg slides on a rough horizontal surface with a deceleration of \displaystyle 1\textrm{.}8 \text{ m}{{\text{s}}^{-2} }.

(a) Draw a diagram to show the forces on the block.

(1 mark)

(b) Show that the magnitude of the friction force acting on the block is 3.6 N.

(2 marks)

(c) Calculate the magnitude of the normal reaction force acting on the block.

(2 marks)

(d) Find the coefficient of friction between the block and the surface.

(3 marks)


4. A heavy crate, of mass 200 kg, is pulled along a rough horizontal surface at a constant speed by a rope. The rope is at an angle of \displaystyle 30{}^\circ to the horizontal. The tension in the rope is \displaystyle T newtons. The coefficient of friction between the crate and the surface is 0.6. Model the crate as a particle.

Image:test1.4a.gif

(a) Draw a diagram to show the forces acting on the crate.

(1 mark)

(b) Show that the magnitude of the normal reaction force is \displaystyle \left( 1960-0\textrm{.}5T \right) newtons.

(3 marks)

(c) Find \displaystyle T.

(4 marks)


5. A particle is initially at the origin and has velocity \displaystyle (4\mathbf{i}+3\mathbf{j})\text{ m}{{\text{s}}^{\text{-1}}}. It moves with constant acceleration and 10 seconds later has velocity \displaystyle (5\mathbf{i}-2\mathbf{j})\text{ m}{{\text{s}}^{\text{-1}}}. The unit vectors \displaystyle \mathbf{i} and \displaystyle \mathbf{j} are directed east and north respectively.

(a) Show that the acceleration of the particle is \displaystyle (0\textrm{.}1\mathbf{i}-0\textrm{.}5\mathbf{j})\text{ m}{{\text{s}}^{\text{-2}}}.

(3 marks)

(b) Find an expression for the position vector of the particle at time t seconds.

(2 marks)

(c) Find the time when the particle is due east of the origin.

(3 marks)

(d) Find the time when the particle is moving due east.

(3 marks)


40 MARKS

Retrieved from "http://wiki.sommarmatte.se/wikis/2009/bridgecoursemechanics/index.php/Practice_Test_Paper_1"