Solution 10.7
From Mechanics
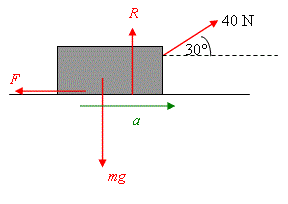
(New page: Image:10.7.gif We have drawn all the forces acting on the block in the figure. The acceleration is represented by the vector <math>a</math>. Applying Newton´s Second Law <math>F=ma<...) |
|||
| Line 8: | Line 8: | ||
& \to :\ 40\cos {{30}^{\circ }}-F=ma \\ | & \to :\ 40\cos {{30}^{\circ }}-F=ma \\ | ||
\end{align}</math> ration is represented by the vector <math>a</math>. | \end{align}</math> ration is represented by the vector <math>a</math>. | ||
| + | |||
| + | Note that <math>R</math> is NOT equal to <math>mg</math> here as the string has a component force in the vertical direction! In fact one has, | ||
| + | |||
| + | <math>\begin{align} | ||
| + | & \uparrow :\ R+40\sin {{30}^{\circ }}-mg=0 \\ | ||
| + | & \\ | ||
| + | & F=mg-40\sin {{30}^{\circ }}=3\times 9\textrm{.}81-40\times \frac{1}{2}=29\textrm{.}43-20=9\textrm{.}43\ \text{N} \\ | ||
| + | \end{align}</math> | ||
| + | |||
| + | Using the friction equation gives | ||
| + | |||
| + | <math>\begin{align} | ||
| + | & F=\mu R \\ | ||
| + | & \\ | ||
| + | & F =0\textrm{.}5 \times 9\textrm{.}43 = 4\textrm{.}72 \ \text{N} \\ | ||
| + | \end{align}</math> | ||
Revision as of 17:11, 14 June 2010
We have drawn all the forces acting on the block in the figure. The acceleration is represented by the vector \displaystyle a.
Applying Newton´s Second Law \displaystyle F=ma horisontally,
\displaystyle \begin{align} & \to :\ 40\cos {{30}^{\circ }}-F=ma \\ \end{align} ration is represented by the vector \displaystyle a.
Note that \displaystyle R is NOT equal to \displaystyle mg here as the string has a component force in the vertical direction! In fact one has,
\displaystyle \begin{align} & \uparrow :\ R+40\sin {{30}^{\circ }}-mg=0 \\ & \\ & F=mg-40\sin {{30}^{\circ }}=3\times 9\textrm{.}81-40\times \frac{1}{2}=29\textrm{.}43-20=9\textrm{.}43\ \text{N} \\ \end{align}
Using the friction equation gives
\displaystyle \begin{align} & F=\mu R \\ & \\ & F =0\textrm{.}5 \times 9\textrm{.}43 = 4\textrm{.}72 \ \text{N} \\ \end{align}