From Mechanics

Revision as of 12:09, 18 May 2010 (edit) Ian (Talk | contribs) (New page: Image:9.5.gif In the figure <math>R1</math> is the air resistance. Resolving up the plane <math>\begin{align} & F1+F-mg\sin {{30}^{\circ }}=0 \\ & \\ & F1=mg-F\sin {{30}^{\circ ...) ← Previous diff		Revision as of 12:42, 18 May 2010 (edit) (undo) Ian (Talk | contribs) Next diff →
Line 5:		Line 5:
	Resolving up the plane		Resolving up the plane
		+	<math>\begin{align}
		+	& F1+F-mg\sin {{20}^{\circ }}=0 \\
		+	& \\
		+	& F1=mg\sin {{20}^{\circ }}-F=60\times 9\textrm{.}81\times 0\textrm{.}342-F=201\textrm{.}3\ \text{N}-F \\
		+	\end{align}</math>
		+
		+	Resolving perpendicular to the plane upwards
	<math>\begin{align}		<math>\begin{align}
-	& F1+F-mg\sin {{30}^{\circ }}=0 \\	+	& R-mg\cos {{20}^{\circ }}=0 \\
	& \\		& \\
-	& F1=mg-F\sin {{30}^{\circ }}=60\times 9.81-\frac{1}{2}F \\	+	& R=mg\cos {{20}^{\circ }}=60\times 9\textrm{.}81\times 0\textrm{.}94=553\ \text{N} \\
	\end{align}</math>		\end{align}</math>
		+
		+	Using the friction equation gives
		+
		+	<math>F=\mu R=0\textrm{.}05\times 553=27\textrm{.}65\ \text{N}</math>
		+
		+	Substituting in the above equation for <math>R1</math> gives
		+
		+	<math>F1=201\textrm{.}3-27\textrm{.}65\approx 173\ \text{N}</math>

---

Revision as of 12:42, 18 May 2010

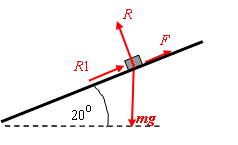
In the figure \displaystyle R1 is the air resistance.

Resolving up the plane

\displaystyle \begin{align} & F1+F-mg\sin {{20}^{\circ }}=0 \\ & \\ & F1=mg\sin {{20}^{\circ }}-F=60\times 9\textrm{.}81\times 0\textrm{.}342-F=201\textrm{.}3\ \text{N}-F \\ \end{align}

Resolving perpendicular to the plane upwards

\displaystyle \begin{align} & R-mg\cos {{20}^{\circ }}=0 \\ & \\ & R=mg\cos {{20}^{\circ }}=60\times 9\textrm{.}81\times 0\textrm{.}94=553\ \text{N} \\ \end{align}

Using the friction equation gives

\displaystyle F=\mu R=0\textrm{.}05\times 553=27\textrm{.}65\ \text{N}

Substituting in the above equation for \displaystyle R1 gives

\displaystyle F1=201\textrm{.}3-27\textrm{.}65\approx 173\ \text{N}