Processing Math: Done
To print higher-resolution math symbols, click the
Hi-Res Fonts for Printing button on the jsMath control panel.
No jsMath TeX fonts found -- using image fonts instead.
These may be slow and might not print well.
Use the jsMath control panel to get additional information.
jsMath Control PanelHide this Message

jsMath

10.2 Underrum

SamverkanLinalgLIU

(Skillnad mellan versioner)
Hoppa till: navigering, sök
Nuvarande version (12 september 2011 kl. 14.35) (redigera) (ogör)
 
Rad 13: Rad 13:
Läs textavsnitt [http://wiki.math.se/wikis/samverkan/linalg-LIU/img_auth.php/6/6c/Kap10_2.pdf 10.2 Definition av underrum].
Läs textavsnitt [http://wiki.math.se/wikis/samverkan/linalg-LIU/img_auth.php/6/6c/Kap10_2.pdf 10.2 Definition av underrum].
- 
-
Du har nu läst definitionen av underrum och här kommer några övningar som testar om du har tagit till dig stoffet.
 
Rad 20: Rad 18:
<imagemap>
<imagemap>
-
Bild:Underrum.png|350px|alt=Alt text
+
Bild:Underrum.png|450px|alt=Alt text
default [http://webcourses.itn.liu.se/webkurs/Underrum.jnlp Du kan visualisera underrum]
default [http://webcourses.itn.liu.se/webkurs/Underrum.jnlp Du kan visualisera underrum]
</imagemap>
</imagemap>

Nuvarande version

       10.1          10.2          10.3          10.4          10.5          10.6          10.7      


Läs textavsnitt 10.2 Definition av underrum.


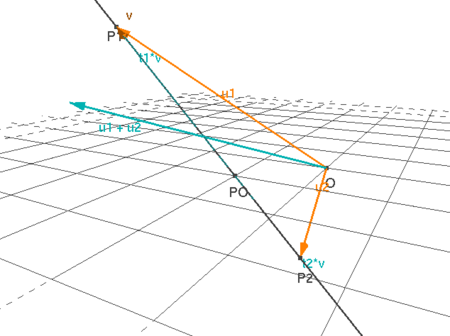
Innan Du börjar arbeta med detta moment så kan Du visualisera underrum genom att klicka på bilden.

alt=Alt textBildinformation


Övning 11.2

Vilka av följande mängder är underrum i R3?

a) M1=R3: x1−2x2+3x3=0

b) M2=R3: x1−2x2+3x3=1

c) M3=R3: x1−2x2+3x3=0ochx2−x3=0

d) M4=R3: x1=0ellerx2=0

Svar | Tips och lösning till a) | Tips och lösning till b) | Tips och lösning till c) | Tips och lösning till d)

Den här artikeln är hämtad från http://wiki.sommarmatte.se/wikis/samverkan/linalg-LIU/index.php/10.2_Underrum