12.3 Tillämpningar
SamverkanLinalgLIU
(Skillnad mellan versioner)
| (2 mellanliggande versioner visas inte.) | |||
| Rad 20: | Rad 20: | ||
| + | __TOC__ | ||
| + | <div class="ovning"> | ||
===Övning 13.18=== | ===Övning 13.18=== | ||
| + | Låt <math>W=[\boldsymbol{v}_1=(1,-1,0)^t,\boldsymbol{v}_2=(1,0,-1)^t]\subset{\bf E}^3</math>. | ||
| + | Låt <math>\boldsymbol{u}=(x_1,x_2,x_3)^t</math>. | ||
| + | Bestäm ortogonala projektionerna <math>P_W(\boldsymbol{u})=\boldsymbol{u}_{\parallel W}</math> | ||
| + | och <math>P_W(\boldsymbol{u})=\boldsymbol{u}_{W^\perp}</math>. | ||
| + | </div>{{#NAVCONTENT:Svar|Svar till U 13.18|Tips och lösning|Tips och lösning till U 13.18}} | ||
Nuvarande version
| 12.1 | 12.2 | 12.3 |
Läs textavsnitt 12.3 Tillämpningar.
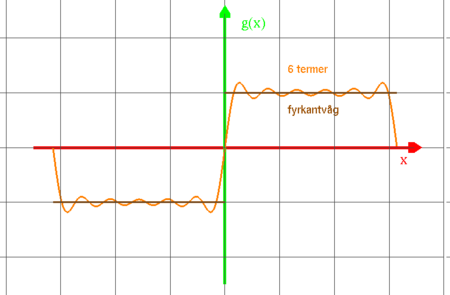
Innan Du börjar arbeta med detta moment så kan Du visualisera Fourierserier genom att klicka på bilden.
Innehåll |
Övning 13.18
Låt \displaystyle W=[\boldsymbol{v}_1=(1,-1,0)^t,\boldsymbol{v}_2=(1,0,-1)^t]\subset{\bf E}^3. Låt \displaystyle \boldsymbol{u}=(x_1,x_2,x_3)^t. Bestäm ortogonala projektionerna \displaystyle P_W(\boldsymbol{u})=\boldsymbol{u}_{\parallel W} och \displaystyle P_W(\boldsymbol{u})=\boldsymbol{u}_{W^\perp}.
Svar
Tips och lösning

 Hämtar...
Hämtar...