Exempel 3.2
Förberedande kurs i matematik
(Skillnad mellan versioner)
Samuel (Diskussion | bidrag)
(Ny sida: ===Exempel 3.2.a=== Bild:Exempel_3.2a.png Låt <math> X=\{ a,b,c,d\}</math> och låt <math> Y=\{1,2,3,4\}</math>. Låt <math>\qquad f(a)=1, f(a)=2, f(b)=2, f(c)=3, f(d)=3</math> Då...)
Gå till nästa ändring →
Versionen från 29 juni 2012 kl. 09.20
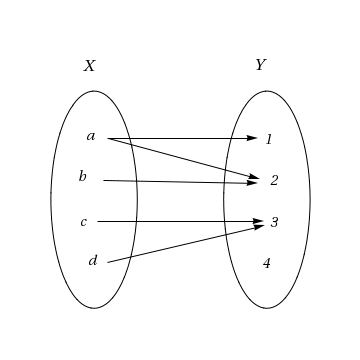
Exempel 3.2.a
Låt \displaystyle X=\{ a,b,c,d\} och låt \displaystyle Y=\{1,2,3,4\}. Låt
\displaystyle \qquad f(a)=1, f(a)=2, f(b)=2, f(c)=3, f(d)=3
Då är inte \displaystyle f en funktion från X till Y, eftersom f(a) inte är unikt bestämt.
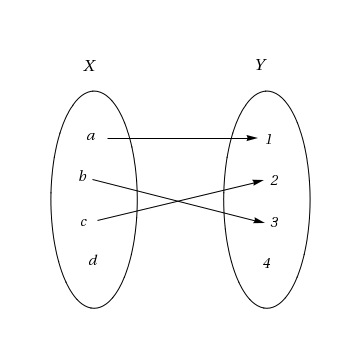
Exempel 3.2.b
Låt \displaystyle X=\{ a,b,c,d\} och låt \displaystyle Y=\{1,2,3,4\}. Låt
\displaystyle \qquad f(a)=1, f(b)=3, f(c)=2
Då är inte \displaystyle f en funktion från X till Y, eftersom det saknas en avbildning för elementet d.