Förberedande kurs i matematik

Exempel 3.2.a

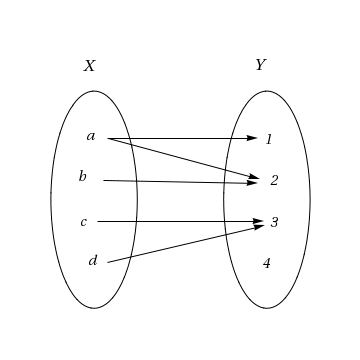
Låt \displaystyle X=\{ a,b,c,d\} och låt \displaystyle Y=\{1,2,3,4\}. Låt

\displaystyle \qquad f(a)=1,\quad f(a)=2, \quad f(b)=2,\quad f(c)=3,\quad f(d)=3

Då är inte \displaystyle f en funktion från \displaystyle X till \displaystyle Y, eftersom \displaystyle f(a) inte är unikt bestämt.

Exempel 3.2.b

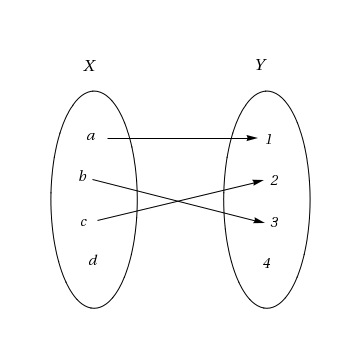
Låt \displaystyle X=\{ a,b,c,d\} och låt \displaystyle Y=\{1,2,3,4\}. Låt

\displaystyle \qquad f(a)=1,\quad f(b)=3,\quad f(c)=2

Då är inte \displaystyle f en funktion från \displaystyle X till \displaystyle Y, eftersom det saknas en avbildning för elementet \displaystyle d.