Inlämningsuppgifter
Förberedande kurs i matematik
| Rad 2: | Rad 2: | ||
[[Bild:Inlupp31_1.png]] | [[Bild:Inlupp31_1.png]] | ||
| - | Låt <math>A=\{a,b,c\}</math>, <math>B=\{a,b,c,d,e\}</math> och <math>C=\{a,b,c,d\}</math>. Låt <math>g:A\to B | + | Låt <math>A=\{a,b,c\}</math>, <math>B=\{a,b,c,d,e\}</math> och <math>C=\{a,b,c,d\}</math>. Låt <math>g:A\to B</math> och <math>f:B\to C</math> vara två funktioner sådana att: |
| - | <math> | + | |
| - | g(a)=a\qquad g(b)=c\qquad g(c)=c | + | <math>\qquad g(a)=a\qquad g(b)=c\qquad g(c)=c</math> |
| - | </math> | + | |
| - | <math> | + | <math>\qquad f(a)=a\qquad f(b)=b\qquad f(c)=c\qquad f(d)=d\qquad f(e)=b</math> |
| - | f(a)=a\qquad f(b)=b\qquad f(c)=c\qquad f(d)=d\qquad f(e)=b | + | |
| - | </math> | + | Dessa funktioner illustreras i bilden ovan. Sätt <math>h(a)=f(g(a))</math>. |
| - | Dessa funktioner illustreras i bilden ovan. Sätt <math>h(a)=f(g(a))</math>. | + | |
a) Bestäm <math>h</math>:s definitionsmängd och dess målmängd. Motivera ditt svar. | a) Bestäm <math>h</math>:s definitionsmängd och dess målmängd. Motivera ditt svar. | ||
| Rad 18: | Rad 18: | ||
d) Är <math>h</math> injektiv? Är den surjektiv? Motivera ditt svar. | d) Är <math>h</math> injektiv? Är den surjektiv? Motivera ditt svar. | ||
| + | |||
Betrakta istället <math>p:\mathbb{Z}\to\mathbb{N}</math> och <math>q:\mathbb{N}\to\mathbb{R}</math> sådana att | Betrakta istället <math>p:\mathbb{Z}\to\mathbb{N}</math> och <math>q:\mathbb{N}\to\mathbb{R}</math> sådana att | ||
| - | <math> | + | |
| - | p(a)=a^2 | + | <math>\qquad p(a)=a^2</math> |
| - | </math> | + | |
| - | <math> | + | <math>\qquad q(a)=\sqrt{a}</math> |
| - | q(a)=\sqrt{a} | + | |
| - | </math> | + | |
Sätt <math>r(a)=q(p(a))</math>. | Sätt <math>r(a)=q(p(a))</math>. | ||
| + | |||
e) Bestäm <math>r</math>:s definitionsmängd och dess målmängd. Motivera ditt svar. | e) Bestäm <math>r</math>:s definitionsmängd och dess målmängd. Motivera ditt svar. | ||
| Rad 38: | Rad 39: | ||
Låt <math>A=\{a,b,c\}</math>, <math>B=\{a,b,c,d,e\}</math> och <math>C=\{a,b,c,d\}</math>. Låt <math>g:A\to B</math> och <math>f:B\to C</math> vara två funktioner sådana att: | Låt <math>A=\{a,b,c\}</math>, <math>B=\{a,b,c,d,e\}</math> och <math>C=\{a,b,c,d\}</math>. Låt <math>g:A\to B</math> och <math>f:B\to C</math> vara två funktioner sådana att: | ||
| - | <math> | + | <math>\qquad g(a)=b\qquad g(b)=b\qquad g(c)=b</math> |
| - | g(a)=b\qquad g(b)=b\qquad g(c)=b | + | |
| - | </math> | + | <math>\qquad f(a)=a\qquad f(b)=a\qquad f(c)=a\qquad f(d)=a\qquad f(e)=a</math> |
| - | <math> | + | |
| - | f(a)=a\qquad f(b)=a\qquad f(c)=a\qquad f(d)=a\qquad f(e)=a | + | |
| - | </math> | + | |
Dessa funktioner illustreras i bilden ovan. Sätt <math>h(a)=f(g(a))</math>. | Dessa funktioner illustreras i bilden ovan. Sätt <math>h(a)=f(g(a))</math>. | ||
| Rad 56: | Rad 54: | ||
Betrakta istället <math>p:\mathbb{N}\to\mathbb{R}</math> och <math>q:\mathbb{R}\to\mathbb{C}</math> sådana att | Betrakta istället <math>p:\mathbb{N}\to\mathbb{R}</math> och <math>q:\mathbb{R}\to\mathbb{C}</math> sådana att | ||
| - | <math> | + | |
| - | p(a)=a^2 | + | <math>\qquad p(a)=a^2</math> |
| - | </math> | + | |
| - | <math> | + | <math>\qquad q(a)=-a</math> |
| - | q(a)=-a | + | |
| - | </math> | + | |
Sätt <math>r(a)=q(p(a))</math>. | Sätt <math>r(a)=q(p(a))</math>. | ||
| Rad 74: | Rad 71: | ||
Låt <math>A=\{a,b,c\}</math>, <math>B=\{a,b,c,d\}</math> och <math>C=\{a,b,c,d,e\}</math>. Låt <math>g:A\to C</math> och <math>f:C\to B</math> vara två funktioner sådana att: | Låt <math>A=\{a,b,c\}</math>, <math>B=\{a,b,c,d\}</math> och <math>C=\{a,b,c,d,e\}</math>. Låt <math>g:A\to C</math> och <math>f:C\to B</math> vara två funktioner sådana att: | ||
| - | <math> | + | |
| - | g(a)=b\qquad g(b)=c\qquad g(c)=d | + | <math>\qquad g(a)=b\qquad g(b)=c\qquad g(c)=d</math> |
| - | </math> | + | |
| - | <math> | + | <math>\qquad f(a)=d\qquad f(b)=a\qquad f(c)=b\qquad f(d)=c\qquad f(e)=d</math> |
| - | f(a)=d\qquad f(b)=a\qquad f(c)=b\qquad f(d)=c\qquad f(e)=d | + | |
| - | </math> | + | Dessa funktioner illustreras i bilden ovan. Sätt <math>h(a)=f(g(a))</math>. |
| - | Dessa funktioner illustreras i bilden ovan. Sätt <math>h(a)=f(g(a))</math>. | + | |
a) Bestäm <math>h</math>:s definitionsmängd och dess målmängd. Motivera ditt svar. | a) Bestäm <math>h</math>:s definitionsmängd och dess målmängd. Motivera ditt svar. | ||
| Rad 92: | Rad 88: | ||
Betrakta istället <math>p:\mathbb{N}\to\mathbb{R}</math> och <math>q:\mathbb{R}\to\mathbb{C}</math> sådana att | Betrakta istället <math>p:\mathbb{N}\to\mathbb{R}</math> och <math>q:\mathbb{R}\to\mathbb{C}</math> sådana att | ||
| - | p(a)=2a | + | <math>\qquad p(a)=2a</math> |
| - | </math> | + | |
| - | q(a)=a+1 | + | <math>\qquad q(a)=a+1</math> |
| - | </math> | + | |
| - | Sätt <math>r(a)=q(p(a))</math>. | + | Sätt <math>r(a)=q(p(a))</math>. |
e) Bestäm <math>r</math>:s definitionsmängd och dess målmängd. Motivera ditt svar. | e) Bestäm <math>r</math>:s definitionsmängd och dess målmängd. Motivera ditt svar. | ||
| Rad 107: | Rad 102: | ||
===Inlämningsuppgift 3.1:4=== | ===Inlämningsuppgift 3.1:4=== | ||
[[Bild:Inlupp31_4.png]] | [[Bild:Inlupp31_4.png]] | ||
| + | |||
Låt <math>A=\{a,b,c,d\}</math>, <math>B=\{a,b,c\}</math> och <math>C=\{a,b,c,d,e\}</math>. Låt <math>g:B\to C</math> och <math>f:C\to A</math> vara två funktioner sådana att: | Låt <math>A=\{a,b,c,d\}</math>, <math>B=\{a,b,c\}</math> och <math>C=\{a,b,c,d,e\}</math>. Låt <math>g:B\to C</math> och <math>f:C\to A</math> vara två funktioner sådana att: | ||
| - | <math> | + | |
| - | g(a)=a\qquad g(b)=c\qquad g(c)=c | + | <math>\qquad g(a)=a\qquad g(b)=c\qquad g(c)=c</math> |
| - | </math> | + | |
| - | <math> | + | <math>\qquad f(a)=a\qquad f(b)=b\qquad f(c)=c\qquad f(d)=d\qquad f(e)=b</math> |
| - | f(a)=a\qquad f(b)=b\qquad f(c)=c\qquad f(d)=d\qquad f(e)=b | + | |
| - | </math> | + | |
Dessa funktioner illustreras i bilden ovan. Sätt <math>h(a)=f(g(a))</math>. | Dessa funktioner illustreras i bilden ovan. Sätt <math>h(a)=f(g(a))</math>. | ||
| Rad 125: | Rad 120: | ||
Betrakta istället <math>p:\mathbb{N}\to\mathbb{R}</math> och <math>q:\mathbb{R}\to\mathbb{C}</math> sådana att | Betrakta istället <math>p:\mathbb{N}\to\mathbb{R}</math> och <math>q:\mathbb{R}\to\mathbb{C}</math> sådana att | ||
| - | <math> | + | |
| - | p(a)=\sqrt{a} | + | <math>\qquad p(a)=\sqrt{a}</math> |
| - | </math> | + | |
| - | <math> | + | <math>\qquad q(a)=a</math> |
| - | q(a)=a | + | |
| - | </math> | + | |
Sätt <math>r(a)=q(p(a))</math>. | Sätt <math>r(a)=q(p(a))</math>. | ||
Versionen från 9 augusti 2012 kl. 13.00
Innehåll |
Inlämningsuppgift 3.1:1
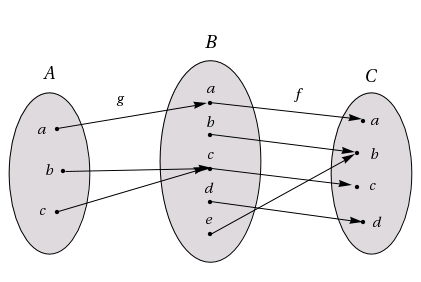
Låt \displaystyle A=\{a,b,c\}, \displaystyle B=\{a,b,c,d,e\} och \displaystyle C=\{a,b,c,d\}. Låt \displaystyle g:A\to B och \displaystyle f:B\to C vara två funktioner sådana att:
\displaystyle \qquad g(a)=a\qquad g(b)=c\qquad g(c)=c
\displaystyle \qquad f(a)=a\qquad f(b)=b\qquad f(c)=c\qquad f(d)=d\qquad f(e)=b
Dessa funktioner illustreras i bilden ovan. Sätt \displaystyle h(a)=f(g(a)).
a) Bestäm \displaystyle h:s definitionsmängd och dess målmängd. Motivera ditt svar.
b) Bestäm \displaystyle h:s värdemängd. Motivera ditt svar.
c) Vad är skillnaden mellan en funktions målmängd och värdemängd?
d) Är \displaystyle h injektiv? Är den surjektiv? Motivera ditt svar.
Betrakta istället \displaystyle p:\mathbb{Z}\to\mathbb{N} och \displaystyle q:\mathbb{N}\to\mathbb{R} sådana att
\displaystyle \qquad p(a)=a^2
\displaystyle \qquad q(a)=\sqrt{a}
Sätt \displaystyle r(a)=q(p(a)).
e) Bestäm \displaystyle r:s definitionsmängd och dess målmängd. Motivera ditt svar.
f) Bestäm \displaystyle r:s värdemängd. Motivera ditt svar.
g) Är \displaystyle r injektiv? Är den surjektiv? Motivera ditt svar.
Inlämningsuppgift 3.1:2
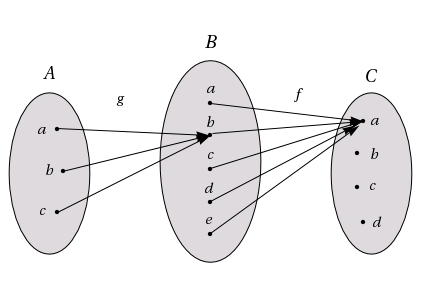 Låt \displaystyle A=\{a,b,c\}, \displaystyle B=\{a,b,c,d,e\} och \displaystyle C=\{a,b,c,d\}. Låt \displaystyle g:A\to B och \displaystyle f:B\to C vara två funktioner sådana att:
Låt \displaystyle A=\{a,b,c\}, \displaystyle B=\{a,b,c,d,e\} och \displaystyle C=\{a,b,c,d\}. Låt \displaystyle g:A\to B och \displaystyle f:B\to C vara två funktioner sådana att:
\displaystyle \qquad g(a)=b\qquad g(b)=b\qquad g(c)=b
\displaystyle \qquad f(a)=a\qquad f(b)=a\qquad f(c)=a\qquad f(d)=a\qquad f(e)=a
Dessa funktioner illustreras i bilden ovan. Sätt \displaystyle h(a)=f(g(a)).
a) Bestäm \displaystyle h:s definitionsmängd och dess målmängd. Motivera ditt svar.
b) Bestäm \displaystyle h:s värdemängd. Motivera ditt svar.
c) Vad är skillnaden mellan en funktions målmängd och värdemängd?
d) Är \displaystyle h injektiv? Är den surjektiv? Motivera ditt svar.
Betrakta istället \displaystyle p:\mathbb{N}\to\mathbb{R} och \displaystyle q:\mathbb{R}\to\mathbb{C} sådana att
\displaystyle \qquad p(a)=a^2
\displaystyle \qquad q(a)=-a
Sätt \displaystyle r(a)=q(p(a)).
e) Bestäm \displaystyle r:s definitionsmängd och dess målmängd. Motivera ditt svar.
f) Bestäm \displaystyle r:s värdemängd. Motivera ditt svar.
g) Är \displaystyle r injektiv? Är den surjektiv? Motivera ditt svar.
Inlämningsuppgift 3.1:3
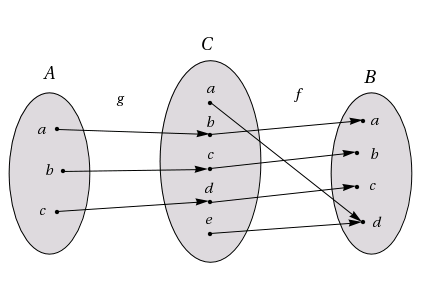
Låt \displaystyle A=\{a,b,c\}, \displaystyle B=\{a,b,c,d\} och \displaystyle C=\{a,b,c,d,e\}. Låt \displaystyle g:A\to C och \displaystyle f:C\to B vara två funktioner sådana att:
\displaystyle \qquad g(a)=b\qquad g(b)=c\qquad g(c)=d
\displaystyle \qquad f(a)=d\qquad f(b)=a\qquad f(c)=b\qquad f(d)=c\qquad f(e)=d
Dessa funktioner illustreras i bilden ovan. Sätt \displaystyle h(a)=f(g(a)).
a) Bestäm \displaystyle h:s definitionsmängd och dess målmängd. Motivera ditt svar.
b) Bestäm \displaystyle h:s värdemängd. Motivera ditt svar.
c) Vad är skillnaden mellan en funktions målmängd och värdemängd?
d) Är \displaystyle h injektiv? Är den surjektiv? Motivera ditt svar.
Betrakta istället \displaystyle p:\mathbb{N}\to\mathbb{R} och \displaystyle q:\mathbb{R}\to\mathbb{C} sådana att
\displaystyle \qquad p(a)=2a
\displaystyle \qquad q(a)=a+1
Sätt \displaystyle r(a)=q(p(a)).
e) Bestäm \displaystyle r:s definitionsmängd och dess målmängd. Motivera ditt svar.
f) Bestäm \displaystyle r:s värdemängd. Motivera ditt svar.
g) Är \displaystyle r injektiv? Är den surjektiv? Motivera ditt svar.
Inlämningsuppgift 3.1:4
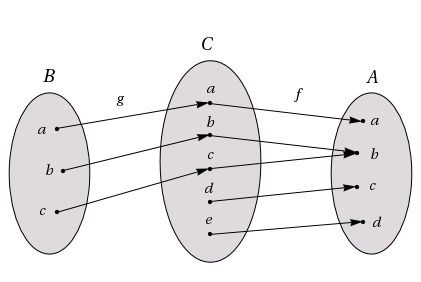
Låt \displaystyle A=\{a,b,c,d\}, \displaystyle B=\{a,b,c\} och \displaystyle C=\{a,b,c,d,e\}. Låt \displaystyle g:B\to C och \displaystyle f:C\to A vara två funktioner sådana att:
\displaystyle \qquad g(a)=a\qquad g(b)=c\qquad g(c)=c
\displaystyle \qquad f(a)=a\qquad f(b)=b\qquad f(c)=c\qquad f(d)=d\qquad f(e)=b
Dessa funktioner illustreras i bilden ovan. Sätt \displaystyle h(a)=f(g(a)).
a) Bestäm \displaystyle h:s definitionsmängd och dess målmängd. Motivera ditt svar.
b) Bestäm \displaystyle h:s värdemängd. Motivera ditt svar.
c) Vad är skillnaden mellan en funktions målmängd och värdemängd?
d) Är \displaystyle h injektiv? Är den surjektiv? Motivera ditt svar.
Betrakta istället \displaystyle p:\mathbb{N}\to\mathbb{R} och \displaystyle q:\mathbb{R}\to\mathbb{C} sådana att
\displaystyle \qquad p(a)=\sqrt{a}
\displaystyle \qquad q(a)=a Sätt \displaystyle r(a)=q(p(a)).
e) Bestäm \displaystyle r:s definitionsmängd och dess målmängd. Motivera ditt svar.
f) Bestäm \displaystyle r:s värdemängd. Motivera ditt svar.
g) Är \displaystyle r injektiv? Är den surjektiv? Motivera ditt svar.
Inlämningsuppgift 5:1
Euklides algoritm och diofantiska ekvationer
1. Ge ett exempel som illustrerar Lemma 1.
2. Använd Euklides algoritm för att bestämma SGD(2345, 245). Redovisa din lösning.
3. Använd Euklides algoritm till att förkorta så \displaystyle \frac{27}{2367} långt som möjligt. Redovisa din lösning.
4. Bestäm alla heltalslösningar till följande ekvationer: \displaystyle 4x + 8y=28 och \displaystyle 4x + 8y=7. Redovisa din lösning.
5. Lille Per har av sin moder fått 100 kr för att gå till konditoriet och köpa lyxsemlor till ett pris av 25kr per styck och mandelkakor till ett pris av 18 kr per styck. När han är framme i konditoriet har han hunnit glömma hur många av de två slagen bakverk han skulle köpa. Han minns dock att inga pengar skulle bli över och att antalet mandelkakor var ett udda tal. Hjälp lille Per!
Inlämningsuppgift 5:2
Euklides algoritm och diofantiska ekvationer
1. Ge ett exempel som illustrerar Lemma 1.
2. Använd Euklides algoritm för att bestämma SGD(569, 31). Redovisa din lösning.
3. Använd Euklides algoritm till att förkorta så \displaystyle \frac{9876}{32} långt som möjligt. Redovisa din lösning.
4. Bestäm alla heltalslösningar till följande ekvationer: \displaystyle 11x + 22y=32 och \displaystyle 11x + 22y=33. Redovisa din lösning.
5. Lille Per har av sin moder fått 120 kr för att gå till konditoriet och köpa lyxsemlor till ett pris av 18kr per styck och mandelkakor till ett pris av 12 kr per styck. När han är framme i konditoriet har han hunnit glömma hur många av de två slagen bakverk han skulle köpa. Han minns dock att inga pengar skulle bli över och att han skulle köpa fler mandelkakor än lyxsemlor. Hjälp lille Per!