Förberedande kurs i matematik

Innehåll 1 Inlämningsuppgift 2 1.1 Inlämningsuppgift 2:1 1.2 Inlämningsuppgift 2:2 1.3 Inlämningsuppgift 2:3 1.4 Inlämningsuppgift 2:4 1.5 Inlämningsuppgift 2:5 1.6 Inlämningsuppgift 2:6 1.7 Inlämningsuppgift 2:7 1.8 Inlämningsuppgift 2:8 2 Inlämningsuppgift 3.1 2.1 Inlämningsuppgift 3.1:1 2.2 Inlämningsuppgift 3.1:2 2.3 Inlämningsuppgift 3.1:3 2.4 Inlämningsuppgift 3.1:4 3 Inlämningsuppgift 3.2 3.1 Inlämningsuppgift 3.2:1 3.2 Inlämningsuppgift 3.2:2 3.3 Inlämningsuppgift 3.2:3 3.4 Inlämningsuppgift 3.2:4 4 Inlämningsuppgift 4.1 4.1 Inlämningsuppgift 4.1:1 4.2 Inlämningsuppgift 4.1:2 5 Inlämningsuppift 4.2 5.1 Inlämningsuppift 4.2:1 5.2 Inlämningsuppift 4.2:2 6 Inlämningsuppgift 5 6.1 Inlämningsuppgift 5:1 (SU) 6.2 Inlämningsuppgift 5:2 (SU) 6.3 Inlämningsuppgift 5:3 (HIG) 6.4 Inlämningsuppgift 5:4 (HIG)

Inlämningsuppgift 2

Kvadratkomplettering:

---

Inlämningsuppgift 2:1

Lös ekvationen \displaystyle 5x^2+4x+1 = 0 med kvadratkomplettering (ej pq-formeln). Använd bråk och inte decimaltal vid uträkningarna. Redovisa din lösning och kontrollera ditt svar genom insättning.

Inlämningsuppgift 2:2

\displaystyle 5x^2+4x-1 = 0

Inlämningsuppgift 2:3

\displaystyle 5x^2-2x+1 = 0

Inlämningsuppgift 2:4

\displaystyle 4x^2+2x-2 = 0

Inlämningsuppgift 2:5

---

Låt \displaystyle p(x)=x^4+x^3+3x-3. Visa att ekvationen \displaystyle p(x)=0 saknar rationella lösningar. Motivera din lösning.

Förslag till inledning är "Enligt kursmaterialet gäller det att om a/b är en rationell rot till ekvationen så måste..."

Inlämningsuppgift 2:6

\displaystyle p(x)=3x^4+x^3+2x-1

Inlämningsuppgift 2:7

\displaystyle p(x)=2x^3+56x-1

Inlämningsuppgift 2:8

\displaystyle p(x)=x^3+5x^2+5

Inlämningsuppgift 3.1

Inlämningsuppgift 3.1:1

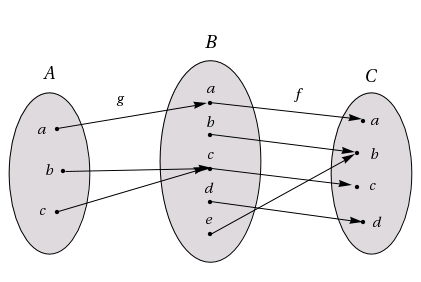
Låt \displaystyle A=\{a,b,c\}, \displaystyle B=\{a,b,c,d,e\} och \displaystyle C=\{a,b,c,d\}. Låt \displaystyle g:A\to B och \displaystyle f:B\to C vara två funktioner sådana att:

\displaystyle \qquad g(a)=a\qquad g(b)=c\qquad g(c)=c

\displaystyle \qquad f(a)=a\qquad f(b)=b\qquad f(c)=c\qquad f(d)=d\qquad f(e)=b

Dessa funktioner illustreras i bilden ovan. Sätt \displaystyle h(a)=f(g(a)).

a) Bestäm \displaystyle h:s definitionsmängd och dess målmängd. Motivera ditt svar.

b) Bestäm \displaystyle h:s värdemängd. Motivera ditt svar.

c) Vad är skillnaden mellan en funktions målmängd och värdemängd?

d) Är \displaystyle h injektiv? Är den surjektiv? Motivera ditt svar.

Betrakta istället \displaystyle p:\mathbb{Z}\to\mathbb{N} och \displaystyle q:\mathbb{N}\to\mathbb{R} sådana att

\displaystyle \qquad p(a)=a^2

\displaystyle \qquad q(a)=\sqrt{a}

Sätt \displaystyle r(a)=q(p(a)).

e) Bestäm \displaystyle r:s definitionsmängd och dess målmängd. Motivera ditt svar.

f) Bestäm \displaystyle r:s värdemängd. Motivera ditt svar.

g) Är \displaystyle r injektiv? Är den surjektiv? Motivera ditt svar.

Inlämningsuppgift 3.1:2

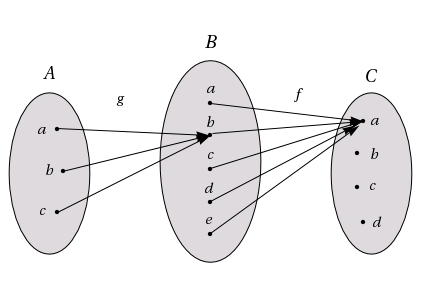
Låt \displaystyle A=\{a,b,c\}, \displaystyle B=\{a,b,c,d,e\} och \displaystyle C=\{a,b,c,d\}. Låt \displaystyle g:A\to B och \displaystyle f:B\to C vara två funktioner sådana att:

\displaystyle \qquad g(a)=b\qquad g(b)=b\qquad g(c)=b

\displaystyle \qquad f(a)=a\qquad f(b)=a\qquad f(c)=a\qquad f(d)=a\qquad f(e)=a

Dessa funktioner illustreras i bilden ovan. Sätt \displaystyle h(a)=f(g(a)).

a) Bestäm \displaystyle h:s definitionsmängd och dess målmängd. Motivera ditt svar.

b) Bestäm \displaystyle h:s värdemängd. Motivera ditt svar.

c) Vad är skillnaden mellan en funktions målmängd och värdemängd?

d) Är \displaystyle h injektiv? Är den surjektiv? Motivera ditt svar.

Betrakta istället \displaystyle p:\mathbb{N}\to\mathbb{R} och \displaystyle q:\mathbb{R}\to\mathbb{R} sådana att

\displaystyle \qquad p(a)=a^2

\displaystyle \qquad q(a)=-a

Sätt \displaystyle r(a)=q(p(a)).

e) Bestäm \displaystyle r:s definitionsmängd och dess målmängd. Motivera ditt svar.

f) Bestäm \displaystyle r:s värdemängd. Motivera ditt svar.

g) Är \displaystyle r injektiv? Är den surjektiv? Motivera ditt svar.

Inlämningsuppgift 3.1:3

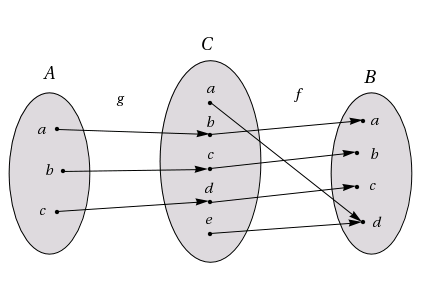
Låt \displaystyle A=\{a,b,c\}, \displaystyle B=\{a,b,c,d\} och \displaystyle C=\{a,b,c,d,e\}. Låt \displaystyle g:A\to C och \displaystyle f:C\to B vara två funktioner sådana att:

\displaystyle \qquad g(a)=b\qquad g(b)=c\qquad g(c)=d

\displaystyle \qquad f(a)=d\qquad f(b)=a\qquad f(c)=b\qquad f(d)=c\qquad f(e)=d

Dessa funktioner illustreras i bilden ovan. Sätt \displaystyle h(a)=f(g(a)).

a) Bestäm \displaystyle h:s definitionsmängd och dess målmängd. Motivera ditt svar.

b) Bestäm \displaystyle h:s värdemängd. Motivera ditt svar.

c) Vad är skillnaden mellan en funktions målmängd och värdemängd?

d) Är \displaystyle h injektiv? Är den surjektiv? Motivera ditt svar.

Betrakta istället \displaystyle p:\mathbb{N}\to\mathbb{Z} och \displaystyle q:\mathbb{Z}\to\mathbb{R} sådana att

\displaystyle \qquad p(a)=2a

\displaystyle \qquad q(a)=a+1

Sätt \displaystyle r(a)=q(p(a)).

e) Bestäm \displaystyle r:s definitionsmängd och dess målmängd. Motivera ditt svar.

f) Bestäm \displaystyle r:s värdemängd. Motivera ditt svar.

g) Är \displaystyle r injektiv? Är den surjektiv? Motivera ditt svar.

Inlämningsuppgift 3.1:4

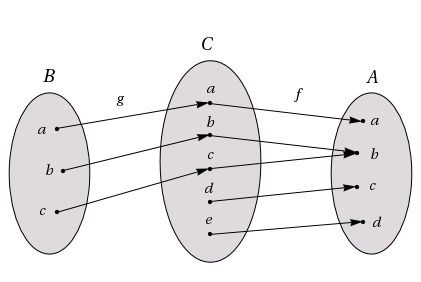
Låt \displaystyle A=\{a,b,c,d\}, \displaystyle B=\{a,b,c\} och \displaystyle C=\{a,b,c,d,e\}. Låt \displaystyle g:B\to C och \displaystyle f:C\to A vara två funktioner sådana att:

\displaystyle \qquad g(a)=a\qquad g(b)=c\qquad g(c)=c

\displaystyle \qquad f(a)=a\qquad f(b)=b\qquad f(c)=c\qquad f(d)=d\qquad f(e)=b

Dessa funktioner illustreras i bilden ovan. Sätt \displaystyle h(a)=f(g(a)).

a) Bestäm \displaystyle h:s definitionsmängd och dess målmängd. Motivera ditt svar.

b) Bestäm \displaystyle h:s värdemängd. Motivera ditt svar.

c) Vad är skillnaden mellan en funktions målmängd och värdemängd?

d) Är \displaystyle h injektiv? Är den surjektiv? Motivera ditt svar.

Betrakta istället \displaystyle p:\mathbb{N}\to\mathbb{R} och \displaystyle q:\mathbb{R}\to\mathbb{C} sådana att

\displaystyle \qquad p(a)=\sqrt{a}

\displaystyle \qquad q(a)=a

Sätt \displaystyle r(a)=q(p(a)).

e) Bestäm \displaystyle r:s definitionsmängd och dess målmängd. Motivera ditt svar.

f) Bestäm \displaystyle r:s värdemängd. Motivera ditt svar.

g) Är \displaystyle r injektiv? Är den surjektiv? Motivera ditt svar.

Inlämningsuppgift 3.2

Inlämningsuppgift 3.2:1

En student har fått uppgiften att lösa ekvationen \displaystyle \sin^2x=1/2. Så här ser studentens lösning ut:

\displaystyle \sin^2x=\frac{1}{2}

\displaystyle \sin x=\frac{1}{\sqrt{2}}

\displaystyle x=45^{\circ}+2n\pi

1. Hitta alla fel i lösningen. Motivera ditt svar.
2. Ge en korrekt lösning.

Inlämningsuppgift 3.2:2

En student har fått uppgiften att lösa ekvationen \displaystyle \sin x\cos x=\cos x. Så här ser studentens lösning ut:

\displaystyle \sin x\cos x=\frac{1}{2}\cos x

\displaystyle \sin x = \frac{1}{2}

\displaystyle x = 30^{\circ}+2n\pi

1. Hitta alla fel i lösningen. Motivera ditt svar.
2. Ge en korrekt lösning.

Inlämningsuppgift 3.2:3

En student har fått uppgiften att lösa ekvationen \displaystyle \sin(-x)=\frac{1}{2}. Så här ser studentens lösning ut:

\displaystyle \sin(-x)=\frac{1}{2}

\displaystyle \sin x = \frac{1}{2}

\displaystyle x = 30^{\circ}+2n\pi

1. Hitta alla fel i lösningen. Motivera ditt svar.
2. Ge en korrekt lösning.

Inlämningsuppgift 3.2:4

En student har fått uppgiften att lösa ekvationen \displaystyle \cos(\pi-x)=\frac{1}{\sqrt{2}}. Så här ser studentens lösning ut:

\displaystyle \cos(\pi-x)=\frac{1}{\sqrt{2}}

\displaystyle \cos x=\frac{1}{\sqrt{2}}

\displaystyle x = 45^{\circ}+2n\pi

1. Hitta alla fel i lösningen. Motivera ditt svar.
2. Ge en korrekt lösning.

Inlämningsuppgift 4.1

Inlämningsuppgift 4.1:1

Låt \displaystyle f(x) = 7, \displaystyle g(x) = x^4 och \displaystyle h(x) = x^5. Visa med hjälp av derivatans definition att

1. \displaystyle f'(x) = 0
2. \displaystyle g'(x) = 4x^3
3. \displaystyle h'(x) = 5x^4
4. \displaystyle D[x^n] = nx^{n-1}. Om du behöver binomialkoefficienter, skriv (n,k) istället av \displaystyle {n\choose k}.

Inlämningsuppgift 4.1:2

Låt \displaystyle f(x) = 6, \displaystyle g(x) = x^4-4 och \displaystyle h(x) = x^5+6. Visa med hjälp av derivatans definition att

1. \displaystyle f'(x) = 0
2. \displaystyle g'(x) = 4x^3
3. \displaystyle h'(x) = 5x^4
4. \displaystyle D[x^n + C] = nx^{n-1}, där \displaystyle n är ett positivt heltal och \displaystyle C en godtycklig konstant. Om du behöver binomialkoefficienter, skriv (n,k) istället av \displaystyle {n\choose k}.

Inlämningsuppift 4.2

Inlämningsuppift 4.2:1

Låt \displaystyle f(x)=\sin(x)+1

1. Beräkna \displaystyle \int_{-\pi}^\pi \! f(x) \ \mathrm{d}x, dvs arean mellan grafen till \displaystyle f(x) och \displaystyle x-axeln som begränsas av linjerna \displaystyle x=-\pi och \displaystyle x=\pi. Du kan skriva I(-pi,pi) istället för \displaystyle \int_{-\pi}^\pi.
2. Beräkna undersumman till \displaystyle f(x) på intervallet \displaystyle [-\pi,\pi] då intervallet delas upp i två lika delar.
3. Beräkna översumman till \displaystyle f(x) på intervallet \displaystyle [-\pi,\pi] då intervallet delas upp i två lika delar.
4. Medelvärdet av under- och översumman kan användas som en uppskattning av arean mellan funktionen och \displaystyle x-axeln på det givna intervallet. Beräkna medelvärdet av under- och översumman och jämför det med den faktiska arean. Är uppskattningen bra?
5. Dela upp intervallet \displaystyle [-\pi,\pi] i fyra lika stora delar och beräkna under- och översumman. Beräkna medelvärdet av under- och översumman. Är detta en bättre uppskattning av än när vi delade upp intervallet i två delar?

Inlämningsuppift 4.2:2

Låt \displaystyle f(x)=x^3+2

1. Beräkna \displaystyle \int_{-1}^2 \! f(x) \ \mathrm{d}x, dvs arean mellan grafen till \displaystyle f(x) och \displaystyle x-axeln som begränsas av linjerna \displaystyle x=-1 och \displaystyle x=2. Du kan skriva I(-1,2) istället för \displaystyle \int_{-1}^2.
2. Beräkna undersumman till \displaystyle f(x) på intervallet \displaystyle [-1,2] då intervallet delas upp i två lika delar.
3. Beräkna översumman till \displaystyle f(x) på intervallet \displaystyle [-1,2] då intervallet delas upp i två lika delar.
4. Medelvärdet av under- och översumman kan användas som en uppskattning av arean mellan funktionen och \displaystyle x-axeln på det givna intervallet. Beräkna medelvärdet av under- och översumman och jämför det med den faktiska arean. Är uppskattningen bra?
5. Dela upp intervallet \displaystyle [-1,3] i sex lika stora delar och beräkna under- och översumman. Beräkna medelvärdet av under- och översumman. Är detta en bättre uppskattning av än när vi delade upp intervallet i två delar?

Inlämningsuppgift 5

Inlämningsuppgift 5:1 (SU)

Decimalutvecklingar och positionssystem

1. Vilken period respektive periodlängd har de rationella talen \displaystyle 1/12, \displaystyle 1/22, \displaystyle 1/82, \displaystyle 1/33?

2. Skriv decimaltalet \displaystyle 0,46454545\dots som en kvot mellan två heltal. Förklara tydligt hur du gör och visa dina beräkningar.

3. Beskriv med egna ord hur man i allmänhet kan gå tillväga för att skriva ett periodiskt decimaltal som ett bråk.

4. Utför följande baskonverteringar:

1. \displaystyle 3030 i bas \displaystyle 6 till bas \displaystyle 10.
2. \displaystyle 3030 i bas \displaystyle 10 till bas \displaystyle 6.
3. \displaystyle 3,030 i bas \displaystyle 6 till bas \displaystyle 10.

Förklara tydligt hur du gör och ta med alla beräkningar.

5. Utför följande beräkningar. Du ska utföra beräkningarna i den givna basen och inte konvertera till bas \displaystyle 10. Förklara tydligt hur du gör och ta med alla beräkningar.

1. \displaystyle 321 + 2300 i bas \displaystyle 4
2. \displaystyle 11\cdot 21 i bas \displaystyle 3
3. \displaystyle 10010 - 1111 i bas \displaystyle 2

6. Sök på nätet efter exempel där man använder tal angivna i bas 16 (det hexadecimala postitionssystemet), och utför en addition i denna bas där två tresiffriga tal adderas.

Euklides algoritm och diofantiska ekvationer

1. Ge ett exempel som illustrerar Lemma 1.

2. Använd Euklides algoritm för att bestämma SGD(2345, 245). Redovisa din lösning.

3. Använd Euklides algoritm till att förkorta så \displaystyle \frac{27}{2367} långt som möjligt. Redovisa din lösning.

4. Bestäm alla heltalslösningar till följande ekvationer: \displaystyle 4x + 8y=28 och \displaystyle 4x + 8y=7. Redovisa din lösning.

5. Lille Per har av sin moder fått 100 kr för att gå till konditoriet och köpa lyxsemlor till ett pris av 25kr per styck och mandelkakor till ett pris av 18 kr per styck. När han är framme i konditoriet har han hunnit glömma hur många av de två slagen bakverk han skulle köpa. Han minns dock att inga pengar skulle bli över och att antalet mandelkakor var ett udda tal. Hjälp lille Per!

Kombinatorik

1a. Permutationen i \displaystyle S_5 som skickar 12345 på 12345 kallas identitetspermutationen. Tag en valfri permutation \displaystyle \sigma\in S_5 skild från identitetspermutationen. Beskriv var \displaystyle \sigma skickar 12345 på och skriv \displaystyle \sigma på cykelnotation. 1b. Tag permutationen \displaystyle \pi som skickar 12345 på 31425 samt permutationen du just valde. Vad skickar \displaystyle \sigma\pi 12345 på? Skriv \displaystyle \sigma\pi med cykelnotation.

2. Ge både ett kombinatoriskt och ett algebraiskt bevis för sambandet

\displaystyle \qquad {n\choose l}{l\choose k}={n\choose k}{n-k\choose l-k}

Tips: till det kombinatoriska beviset: Vänsterledet kan vi exempelvis se som antalet sätt att välja ut l personer ur en grupp på n som får åka på en resa, av de l personerna väljs sedan k ut att få åka första klass.

3a. Beskriv hur urval med återläggning och utan hänsyn till ordning går till och motivera Sats 2 med egna ord (ca 1/3 sida).

3b. Anna har tre sorters tröjor: gröna, röda och svarta. Alla tröjor med samma färg är likadana och Anna har minst tio av varje sort. Till en resa ska Anna ta med sig 9 tröjor. På hur många sätta kan Anna välja vilka tröjor hos ska ta med sig?

3c. Ett annat sätt att formulera uppgift 3b är följande: Hur många lösningar har ekvationen \displaystyle x_1+x_2+x_3=9 där \displaystyle x_1,x_2,x_3\in\mathbb{N}. Vi kan se \displaystyle x_1 som antalet gröna tröjor, \displaystyle x_2 som antalet röda tröjor och \displaystyle x_3 som antalet svarta tröjor. Tillsammans skulle nio tröjor väljas varför summan av de tre variablerna ska vara 9. Använd detta för att ta reda på antalet lösningar i till ekvationen

\displaystyle \qquad x_1+x_2+x_3+x_4=6

Inlämningsuppgift 5:2 (SU)

Decimalutvecklingar och positionssystem

1. Vilken period respektive periodlängd har de rationella talen \displaystyle 1/7, \displaystyle 3/7, \displaystyle 2/7, \displaystyle 1/11?

2. Skriv decimaltalet 0.0234234234234... som en kvot mellan två heltal.

3. Utför följande baskonverteringar:

1. \displaystyle 10 i bas \displaystyle 2 till bas \displaystyle 4.
2. \displaystyle 10 i bas \displaystyle 4 till bas \displaystyle 2.
3. \displaystyle 100,001 i bas \displaystyle 2 till bas \displaystyle 4.

Förklara tydligt hur du gör och ta med alla beräkningar.

4. Beskriv med egna ord hur man i allmänhet kan konvertera ett tal i bas 2 till bas 4. Ta inte ett exempel utan beskriv det allmänna fallet.

5. Utför följande beräkningar. Du ska utföra beräkningarna i den givna basen och inte konvertera till bas \displaystyle 10. Förklara tydligt hur du gör och ta med alla beräkningar.

1. \displaystyle 102,2 + 10,2 i bas \displaystyle 3
2. \displaystyle 12\cdot12 i bas \displaystyle 5
3. \displaystyle 1002 - 210 i bas \displaystyle 3

6. I "Liftarens guide till galaxen" av Douglas Adams lär vi oss att svaret på livet, universum och allt är 42. Senare i samma bokserie försöker protagonisten bestämma vad som i så fall är själva frågan, och lämnar förslaget 'vad är \displaystyle 6 \cdot 9 ?'.

Vi kan snabbt konstatera att \displaystyle 6 \cdot 9 = 54 , så det verkar som om vi har fel fråga. En läsare av boken konstaterade att ekvationen faktiskt stämmer, men i bas 13, på vilket Adams svarade "I may be a sorry case, but I don't write jokes in base 13".

Antag att Adams faktiskt hade gjort det, hur hade vi då beräknat \displaystyle 6 \cdot 9 i bas 13? Låt bas-10 talen 10, 11, 12 representeras av A, B och C och utför beräkningen utan att konvertera till bas 10. Förklara alla steg.

Euklides algoritm och diofantiska ekvationer

1. Ge ett exempel som illustrerar Lemma 1.

2. Använd Euklides algoritm för att bestämma SGD(338, 182). Redovisa din lösning.

3. Använd Euklides algoritm till att förkorta så \displaystyle \frac{11520}{2496} långt som möjligt. Redovisa din lösning.

4. Bestäm alla heltalslösningar till följande ekvationer: \displaystyle 5x + 3y=17 och \displaystyle 5x + 3y=39. Redovisa din lösning.

5. Lille Per har av sin moder fått 120 kr för att gå till konditoriet och köpa lyxsemlor till ett pris av 18kr per styck och mandelkakor till ett pris av 12 kr per styck. När han är framme i konditoriet har han hunnit glömma hur många av de två slagen bakverk han skulle köpa. Han minns dock att inga pengar skulle bli över och att han skulle köpa fler mandelkakor än lyxsemlor. Hjälp lille Per!

Kombinatorik

1a. Permutationen i \displaystyle S_5 som skickar 12345 på 12345 kallas identitetspermutationen. Tag en valfri permutation \displaystyle \sigma\in S_5 skild från identitetspermutationen. Beskriv var \displaystyle \sigma skickar 12345 på och skriv \displaystyle \sigma på cykelnotation. 1b. Tag permutationen \displaystyle \pi som skickar 12345 på 31425 samt permutationen du just valde. Vad skickar \displaystyle \sigma\pi 12345 på? Skriv \displaystyle \sigma\pi med cykelnotation.

2. Ge både ett kombinatoriskt och ett algebraiskt bevis för sambandet

\displaystyle \qquad {n\choose l}{l\choose k}={n\choose k}{n-k\choose l-k}

Tips: till det kombinatoriska beviset: Vänsterledet kan vi exempelvis se som antalet sätt att välja ut l personer ur en grupp på n som får åka på en resa, av de l personerna väljs sedan k ut att få åka första klass.

3a. Beskriv hur urval med återläggning och utan hänsyn till ordning går till och motivera Sats 2 med egna ord (ca 1/3 sida).

3b. Anna har tre sorters tröjor: gröna, röda och svarta. Alla tröjor med samma färg är likadana och Anna har minst tio av varje sort. Till en resa ska Anna ta med sig 9 tröjor. På hur många sätta kan Anna välja vilka tröjor hos ska ta med sig?

3c. Ett annat sätt att formulera uppgift 3b är följande: Hur många lösningar har ekvationen \displaystyle x_1+x_2+x_3=9 där \displaystyle x_1,x_2,x_3\in\mathbb{N}. Vi kan se \displaystyle x_1 som antalet gröna tröjor, \displaystyle x_2 som antalet röda tröjor och \displaystyle x_3 som antalet svarta tröjor. Tillsammans skulle nio tröjor väljas varför summan av de tre variablerna ska vara 9. Använd detta för att ta reda på antalet lösningar i till ekvationen

\displaystyle \qquad x_1+x_2+x_3+x_4=6

Inlämningsuppgift 5:3 (HIG)

Decimalutvecklingar och positionssystem

1. Vilken period respektive periodlängd har de rationella talen \displaystyle 1/35, \displaystyle 1/7, \displaystyle 1/44, \displaystyle 1/60?

2. Skriv decimaltalet \displaystyle 0,16666\dots som en kvot mellan två heltal.

3. Utför följande baskonverteringar:

1. \displaystyle 4242 i bas \displaystyle 7 till bas \displaystyle 10.
2. \displaystyle 4242 i bas \displaystyle 10 till bas \displaystyle 7.
3. \displaystyle 4,24 i bas \displaystyle 7 till bas \displaystyle 10.

Förklara tydligt hur du gör och ta med alla beräkningar.

4. Beskriv med egna ord hur man i allmänhet kan konvertera ett tal i bas 10 till bas 7. Ta inte ett exempel utan beskriv det allmänna fallet.

5. Utför följande beräkningar. Du ska utföra beräkningarna i den givna basen och inte konvertera till bas \displaystyle 10. Förklara tydligt hur du gör och ta med alla beräkningar.

1. \displaystyle 101,1 + 10,1 i bas \displaystyle 2
2. \displaystyle 32\cdot32 i bas \displaystyle 5
3. \displaystyle 1001 - 110 i bas \displaystyle 2

6. Sök på nätet efter exempel där man använder tal angivna i bas 16 (det hexadecimala postitionssystemet), och utför en addition i denna bas där två tresiffriga tal adderas.

Euklides algoritm och diofantiska ekvationer

1. Ge ett exempel som illustrerar Lemma 1.

2. Använd Euklides algoritm för att bestämma SGD(569, 31). Redovisa din lösning.

3. Använd Euklides algoritm till att förkorta så \displaystyle \frac{9876}{32} långt som möjligt. Redovisa din lösning.

4. Bestäm alla heltalslösningar till följande ekvationer: \displaystyle 11x + 22y=32 och \displaystyle 11x + 22y=33. Redovisa din lösning.

5. Lille Per har av sin moder fått 120 kr för att gå till konditoriet och köpa lyxsemlor till ett pris av 18kr per styck och mandelkakor till ett pris av 12 kr per styck. När han är framme i konditoriet har han hunnit glömma hur många av de två slagen bakverk han skulle köpa. Han minns dock att inga pengar skulle bli över och att han skulle köpa fler mandelkakor än lyxsemlor. Hjälp lille Per!

Kombinatorik

1a. Permutationen i \displaystyle S_5 som skickar 12345 på 12345 kallas identitetspermutationen. Tag en valfri permutation \displaystyle \sigma\in S_5 skild från identitetspermutationen. Beskriv var \displaystyle \sigma skickar 12345 på och skriv \displaystyle \sigma på cykelnotation. 1b. Tag permutationen \displaystyle \pi som skickar 12345 på 31425 samt permutationen du just valde. Vad skickar \displaystyle \sigma\pi 12345 på? Skriv \displaystyle \sigma\pi med cykelnotation.

2. Ge både ett kombinatoriskt och ett algebraiskt bevis för sambandet

\displaystyle \qquad {n\choose l}{l\choose k}={n\choose k}{n-k\choose l-k}

Tips: till det kombinatoriska beviset: Vänsterledet kan vi exempelvis se som antalet sätt att välja ut l personer ur en grupp på n som får åka på en resa, av de l personerna väljs sedan k ut att få åka första klass.

3a. Beskriv hur urval med återläggning och utan hänsyn till ordning går till och motivera Sats 2 med egna ord (ca 1/3 sida).

3b. Anna har tre sorters tröjor: gröna, röda och svarta. Alla tröjor med samma färg är likadana och Anna har minst tio av varje sort. Till en resa ska Anna ta med sig 9 tröjor. På hur många sätta kan Anna välja vilka tröjor hos ska ta med sig?

3c. Ett annat sätt att formulera uppgift 3b är följande: Hur många lösningar har ekvationen \displaystyle x_1+x_2+x_3=9 där \displaystyle x_1,x_2,x_3\in\mathbb{N}. Vi kan se \displaystyle x_1 som antalet gröna tröjor, \displaystyle x_2 som antalet röda tröjor och \displaystyle x_3 som antalet svarta tröjor. Tillsammans skulle nio tröjor väljas varför summan av de tre variablerna ska vara 9. Använd detta för att ta reda på antalet lösningar i till ekvationen

\displaystyle \qquad x_1+x_2+x_3+x_4=6

Inlämningsuppgift 5:4 (HIG)

Decimalutvecklingar och positionssystem

1. Vilken period respektive periodlängd har de rationella talen \displaystyle 1/13, \displaystyle 1/40, \displaystyle 2/33, \displaystyle 7/80?

2. Skriv decimaltalet \displaystyle 0,324324324 \dots som en kvot mellan två heltal.

3. Utför följande baskonverteringar:

1. \displaystyle 3133 i bas \displaystyle 7 till bas \displaystyle 10.
2. \displaystyle 4888 i bas \displaystyle 10 till bas \displaystyle 7.
3. \displaystyle 6,46 i bas \displaystyle 7 till bas \displaystyle 10.

Förklara tydligt hur du gör och ta med alla beräkningar.

4. Beskriv med egna ord hur man i allmänhet kan konvertera ett tal i bas 10 till bas 5. Ta inte ett exempel utan beskriv det allmänna fallet.

5. Utför följande beräkningar. Du ska utföra beräkningarna i den givna basen och inte konvertera till bas \displaystyle 10. Förklara tydligt hur du gör och ta med alla beräkningar.

1. \displaystyle 121,1 + 11,1 i bas \displaystyle 2
2. \displaystyle 33\cdot33 i bas \displaystyle 5
3. \displaystyle 1101 - 111 i bas \displaystyle 2

6. Sök på nätet efter exempel där man använder tal angivna i bas 16 (det hexadecimala postitionssystemet), och utför en addition i denna bas där två tresiffriga tal adderas.

Euklides algoritm och diofantiska ekvationer

1. Ge ett exempel som illustrerar Lemma 1.

2. Använd Euklides algoritm för att bestämma SGD(2889, 522). Redovisa din lösning.

3. Använd Euklides algoritm till att förkorta så \displaystyle \frac{4145}{355} långt som möjligt. Redovisa din lösning.

4. Bestäm alla heltalslösningar till följande ekvationer: \displaystyle 13x + 22y=32 och \displaystyle 48x + 64y= 56 . Redovisa din lösning.

5. Lille Per har av sin moder fått 120 kr för att gå till konditoriet och köpa lyxsemlor till ett pris av 18kr per styck och mandelkakor till ett pris av 12 kr per styck. När han är framme i konditoriet har han hunnit glömma hur många av de två slagen bakverk han skulle köpa. Han minns dock att inga pengar skulle bli över och att han skulle köpa fler mandelkakor än lyxsemlor. Hjälp lille Per!

Kombinatorik

1a. Permutationen i \displaystyle S_5 som skickar 12345 på 12345 kallas identitetspermutationen. Tag en valfri permutation \displaystyle \sigma\in S_5 skild från identitetspermutationen. Beskriv var \displaystyle \sigma skickar 12345 på och skriv \displaystyle \sigma på cykelnotation. 1b. Tag permutationen \displaystyle \pi som skickar 12345 på 31425 samt permutationen du just valde. Vad skickar \displaystyle \sigma\pi 12345 på? Skriv \displaystyle \sigma\pi med cykelnotation.

2. Ge både ett kombinatoriskt och ett algebraiskt bevis för sambandet

\displaystyle \qquad {n\choose l}{l\choose k}={n\choose k}{n-k\choose l-k}

Tips: till det kombinatoriska beviset: Vänsterledet kan vi exempelvis se som antalet sätt att välja ut l personer ur en grupp på n som får åka på en resa, av de l personerna väljs sedan k ut att få åka första klass.

3a. Beskriv hur urval med återläggning och utan hänsyn till ordning går till och motivera Sats 2 med egna ord (ca 1/3 sida).

3b. Anna har tre sorters tröjor: gröna, röda och svarta. Alla tröjor med samma färg är likadana och Anna har minst tio av varje sort. Till en resa ska Anna ta med sig 9 tröjor. På hur många sätta kan Anna välja vilka tröjor hos ska ta med sig?

3c. Ett annat sätt att formulera uppgift 3b är följande: Hur många lösningar har ekvationen \displaystyle x_1+x_2+x_3=9 där \displaystyle x_1,x_2,x_3\in\mathbb{N}. Vi kan se \displaystyle x_1 som antalet gröna tröjor, \displaystyle x_2 som antalet röda tröjor och \displaystyle x_3 som antalet svarta tröjor. Tillsammans skulle nio tröjor väljas varför summan av de tre variablerna ska vara 9. Använd detta för att ta reda på antalet lösningar i till ekvationen

\displaystyle \qquad x_1+x_2+x_3+x_4=6