Testsida3
Förberedande kurs i matematik
| Rad 4: | Rad 4: | ||
{| width="100%" cellspacing="10px" | {| width="100%" cellspacing="10px" | ||
Betrakta ekvationen <math>\cos(x)=-\frac{\sqrt{3}}{2}</math>. Vi noterar först och <math>\sqrt{3}/2</math> motsvarar en standarvinkel, nämligen <math>\pi/6</math>. Däremot finns inte <math>-\sqrt{3}/2</math> med på de vanligaste tabellerna över cos- och sin-värden för vanliga vinklar. Hur löser man då den här ekvationen? Vi ska dela upp lösningen i några enklare steg. | Betrakta ekvationen <math>\cos(x)=-\frac{\sqrt{3}}{2}</math>. Vi noterar först och <math>\sqrt{3}/2</math> motsvarar en standarvinkel, nämligen <math>\pi/6</math>. Däremot finns inte <math>-\sqrt{3}/2</math> med på de vanligaste tabellerna över cos- och sin-värden för vanliga vinklar. Hur löser man då den här ekvationen? Vi ska dela upp lösningen i några enklare steg. | ||
| - | | a) Utgå från ekvationen <math>\cos(\pi/3)=\sqrt{3}/2</math>. Använd trigonometriska samband från kurslitteraturen för att skriva om denna ekvation som <math>\cos(x)=-\sqrt{3}/2</math>, där <math>x</math> är en vinkel mellan <math>0</math> och <math> | + | | a) Utgå från ekvationen <math>\cos(\pi/3)=\sqrt{3}/2</math>. Använd trigonometriska samband från kurslitteraturen för att skriva om denna ekvation som <math>\cos(x)=-\sqrt{3}/2</math>, där <math>x</math> är en vinkel mellan <math>0</math> och <math>\pi</math>. |
|- | |- | ||
| b) I a)-uppgift hittade vi en lösning till den angivna ekvationen. Hitta en till lösning på intervallet <math>[0,2\pi)</math>. Tips: rita upp enhetscirkeln! | | b) I a)-uppgift hittade vi en lösning till den angivna ekvationen. Hitta en till lösning på intervallet <math>[0,2\pi)</math>. Tips: rita upp enhetscirkeln! | ||
Versionen från 2 augusti 2012 kl. 11.42
Övning 2.5.1
| a) Utgå från ekvationen \displaystyle \cos(\pi/3)=\sqrt{3}/2. Använd trigonometriska samband från kurslitteraturen för att skriva om denna ekvation som \displaystyle \cos(x)=-\sqrt{3}/2, där \displaystyle x är en vinkel mellan \displaystyle 0 och \displaystyle \pi. |
| b) I a)-uppgift hittade vi en lösning till den angivna ekvationen. Hitta en till lösning på intervallet \displaystyle [0,2\pi). Tips: rita upp enhetscirkeln! |
| c) I deluppgift a) och b) hittade två lösningar till ekvationen. Hitta resten av lösningarna. |
Övning 2.3.4
Övning 4.2.2
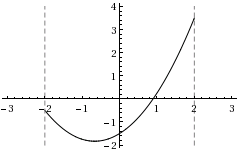
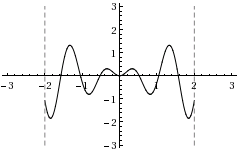
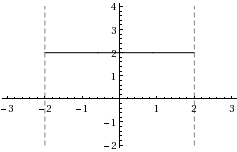
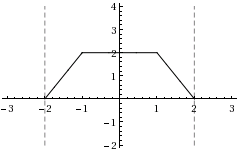
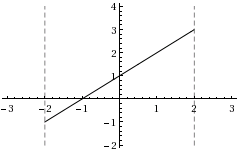
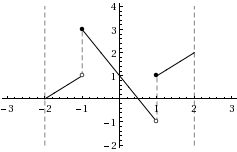
En punkt kallas \displaystyle a ett lokalt minimum om funktionsvärdena precis intill punkten är mindre än eller lika med \displaystyle f(a). På motsvarande sätt definieras ett lokalt maximum. Hitta antalet lokala maximi- och minimipunkter på intervallet \displaystyle (-2,2). Notera att \displaystyle 2 och \displaystyle -2 inte ligger på intervallet.
| a) | \displaystyle f(x)=\frac{3x^2}{4} +x-3/2 | |
| b) | \displaystyle f(x)=x\sin{(6x)} | |
| c) | \displaystyle f(x)=2 | |
| d) | \displaystyle f(x)=\begin{cases}-2x+4&\text{om }x<-1\\2&\text{om }-1\leq x\leq 1\\2x+4&\text{om }x>1\end{cases} | |
| e) | \displaystyle f(x)=x+1 | |
| f) | \displaystyle f(x)=\begin{cases}x+2&\text{om }x<-1\\-2 x + 1&\text{om }-1\leq x< 1\\x&\text{om }x\geq 1\end{cases} |
 Hämtar...
Hämtar...