16.10 Projektioner och speglingar med basbyte
SamverkanLinalgLIU
| 16.1 | 16.2 | 16.3 | 16.4 | 16.5 | 16.6 | 16.7 | 16.8 | 16.9 | 16.10 | 16.11 |
Läs textavsnitt 16.10 Projektioner och speglingar med basbyte
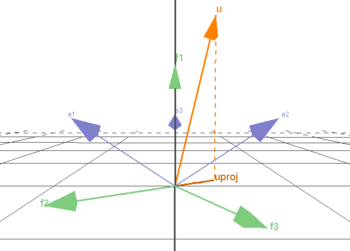
Innan Du börjar arbeta med detta moment så kan Du visualisera ortogonal projektion med hjälp av basbyte genom att klicka på bilden.
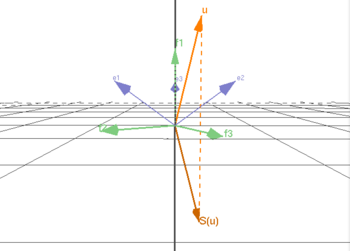
Innan Du börjar arbeta med detta moment så kan Du visualisera spegling med hjälp av basbyte genom att klicka på bilden.
Övningar
17.35. Låt \displaystyle \underline{\boldsymbol{e}}=\{\boldsymbol{e}_1, \boldsymbol{e}_2\} vara en ON-bas i planet. Inför en ny bas \displaystyle \underline{\boldsymbol{f}}=\{\boldsymbol{f}_1, \boldsymbol{f}_2\} genom
\left\{\begin{array}{lcl}\boldsymbol{f}_1&=&\frac{1}{\sqrt5}(\boldsymbol{e}_1+2\boldsymbol{e}_2)\\ \boldsymbol{f}_2&=&\frac{1}{\sqrt5}(2\boldsymbol{e}_1-\boldsymbol{e}_2)\end{array}\right.
Låt \displaystyle F vara ortogonal projektion på linjen \displaystyle x_1+2x_2=0. Ange \displaystyle F:s matris i basen \displaystyle \underline{\boldsymbol{f}} och beräkna med hjälp av bassambandet \displaystyle F:s matris i basen \displaystyle \underline{\boldsymbol{e}}.
Ortogonal projektion med hjälp av basbyte
17.36. Låt \displaystyle \underline{\boldsymbol{e}}=\{\boldsymbol{e}_1, \boldsymbol{e}_2\} vara en ON-bas i planet.
Inför en ny bas \displaystyle \underline{\boldsymbol{f}}=\{\boldsymbol{f}_1, \boldsymbol{f}_2\}
genom
\left\{\begin{array}{lcl}\boldsymbol{f}_1&=&\frac{1}{\sqrt5}(\boldsymbol{e}_1+2\boldsymbol{e}_2)\\ \boldsymbol{f}_2&=&\frac{1}{\sqrt5}(2\boldsymbol{e}_1-\boldsymbol{e}_2)\end{array}\right.
Låt \displaystyle F vara spegling i linjen \displaystyle x_1+2x_2=0. Ange \displaystyle F:s matris i basen \displaystyle \underline{\boldsymbol{f}} och beräkna med hjälp av bassambandet \displaystyle F:s matris i basen \displaystyle \underline{\boldsymbol{e}}.
Reflektionsuppgifter
1. Vad är vitsen med att ha basbyte mellan ON-baser?
2. Beskriv kolonnerna i \displaystyle A_{\boldsymbol{e}} resp \displaystyle A_{\boldsymbol{f}}.

 Hämtar...
Hämtar...