4.3 Tillämpningar
SamverkanLinalgLIU
| 4.1 | 4.2 | 4.3 |
Läs textavsnitt 4.3 Tillämpningar.
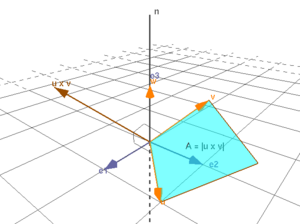
Klicka på bilden för att starta visualiseringen.
Du har nu läst tillämpningar på vektorprodukt och här kommer några övningar som testar om du har tagit till dig stoffet.
Innehåll |
Övning 5.5
Bestäm arean av den triangel som har hörn i \displaystyle (1,1,1) , \displaystyle (1,2,1) och \displaystyle (3,2,1).
Övning 5.6
Bestäm arean för en parallellogram som har hörnpunkterna \displaystyle (1,3,2) , \displaystyle (2,-1,1) , \displaystyle (-1,2,3) och \displaystyle (0,-2,2) .
Övning 5.7
Bestäm arean av en parallellogram som har diagonalvektorerna \displaystyle \boldsymbol{v} =\begin{pmatrix} 2 \\ -5 \\ -3\end{pmatrix} och \displaystyle \boldsymbol{w} = \begin{pmatrix} 4\\ 3\\ -1\end{pmatrix}.
Övning 5.8
Bestäm volymen av den parallellepiped som spänns upp av vektorerna \displaystyle \begin{pmatrix} 3 \\ 1 \\ 7\end{pmatrix},
\displaystyle \begin{pmatrix} 2 \\ -3 \\ 5\end{pmatrix} och \displaystyle \begin{pmatrix} 9 \\ 0 \\ 1\end{pmatrix}.
Övning 5.9
Vilka av följande uppsättningar av vektorer är linjärt beroende?
{\rm a)}\ \begin{pmatrix} 1 \\ 0 \\ 3\end{pmatrix}. \begin{pmatrix} 6 \\ 1 \\ 5\end{pmatrix}. \begin{pmatrix} 8 \\ 1 \\ 11\end{pmatrix} \qquad {\rm b)}\ \begin{pmatrix} 1 \\ 1 \\ 1\end{pmatrix}. \begin{pmatrix} 6 \\ 7 \\ 0\end{pmatrix}. \begin{pmatrix} 1 \\ 2 \\ 3\end{pmatrix}.
Övning 5.10
För vilka \displaystyle a är vektorerna \displaystyle \begin{pmatrix} a \\ 1 \\ 1\end{pmatrix}, \displaystyle \begin{pmatrix} 1 \\ a \\ 2\end{pmatrix} och \displaystyle \begin{pmatrix} 1 \\ 1 \\ a+1\end{pmatrix} linjärt beroende?
Övning 5.11
För vilka \displaystyle t ligger punkterna \displaystyle (t,1,2), \displaystyle (1,t,3), \displaystyle (1,1,1) och \displaystyle (0,1,1) i ett plan?
Övning 5.12
Ange ett värde på talet \displaystyle a så att vektorekvationen
\times \begin{pmatrix} x\\ y \\ z\end{pmatrix} =\begin{pmatrix} 1 \\ a \\ 3\end{pmatrix}
blir lösbar.
Övning 5.13
Antag att \displaystyle \boldsymbol{u} = \begin{pmatrix} 1 \\ -1 \\ 2\end{pmatrix} och \displaystyle \boldsymbol{v} =\begin{pmatrix} -k \\ 1 \\ k\end{pmatrix}. Lös vektorekvationen \displaystyle \boldsymbol{u} \times \boldsymbol{x} = \boldsymbol{v} för alla reella tal \displaystyle k , för vilka ekvationen är lösbar.
Övning 5.14
Låt \displaystyle \boldsymbol{u} = \begin{pmatrix} 1 \\ 1 \\ 2\end{pmatrix} och \displaystyle \boldsymbol{v} = \begin{pmatrix} 2 \\ 1 \\ 1\end{pmatrix}. Bestäm alla lösningar \displaystyle \boldsymbol{x} till ekvationssystemet
\left\{\begin{array}{rcr} \boldsymbol{u} \cdot ( \boldsymbol{x} \times \boldsymbol{v} )&=&0\\ \boldsymbol{u} \cdot \boldsymbol{x} &=&0 \end{array}\right.

 Hämtar...
Hämtar...