16.11 Rotationer
SamverkanLinalgLIU
| Rad 21: | Rad 21: | ||
[[Bild:RotationFilm.png|| |350px]] | [[Bild:RotationFilm.png|| |350px]] | ||
| - | [http://webstaff.itn.liu.se/%7Egeoba/TNA002/webkurs/RotationFilm.jnlp | + | [http://webstaff.itn.liu.se/%7Egeoba/TNA002/webkurs/RotationFilm.jnlp Starta filmvisningen] |
Versionen från 9 mars 2011 kl. 12.31
| 16.1 | 16.2 | 16.3 | 16.4 | 16.5 | 16.6 | 16.7 | 16.8 | 16.9 | 16.10 | 16.11 |
Läs textavsnitt 16.11 Rotationer
För att se en filmvisning om rotation så klicka på länken
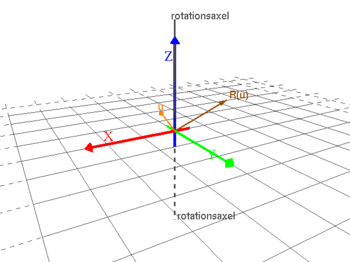
Övningar
17.37 Givet en höger ON-bas i rummet. Följande matriser definierar linjära avbildningar i rummet. Beskriv geometriskt vad dessa gör.
A_1=\left(\begin{array}{rrr} 1&0 & 0\\ 0& 0& 0\\ 0& 0& 1\end{array}\right)\qquad A_2=\left(\begin{array}{rrr} 1& 0& 0\\ 0& 3& 0\\ 0& 0& 1\end{array}\right)\qquad A_3=\left(\begin{array}{rrr} 1& 0& 0\\ 0& \cos\theta& -\sin\theta\\ 0& \sin\theta& \cos\theta\end{array}\right)
17.38 Låt \displaystyle \underline{\boldsymbol{e}} vara en höger ON-bas i rummet och låt en rotationsaxel \displaystyle L vara parallell med vektorn \displaystyle 2\boldsymbol{e}_1+2\boldsymbol{e}_2-\boldsymbol{e}_3.
- Bestäm \displaystyle F:s matris \displaystyle A_{\boldsymbol{e}} om \displaystyle F är en rotation \displaystyle \pi/2 i positiv led runt \displaystyle L.
- Bestäm \displaystyle G:s matris \displaystyle B_{\boldsymbol{e}} om \displaystyle G är en rotation \displaystyle 3\pi/2 i positiv led runt \displaystyle L.
- Bestäm \displaystyle A^4_{\boldsymbol{e}}.
För att visualisera uppgift 17.38 så klicka på länken
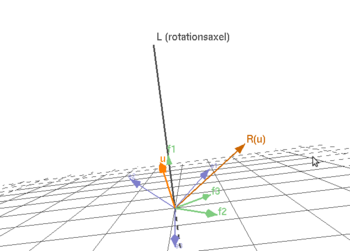
17.39. Låt \displaystyle \underline{\boldsymbol{e}} vara en höger ON-bas i rummet och \displaystyle F rotation \displaystyle 2\pi/3 i positiv led runt \displaystyle \boldsymbol{e}_1+\boldsymbol{e}_2+\boldsymbol{e}_3. Beräkna avbildningens matris i basen \displaystyle \underline{\boldsymbol{e}}.
Reflektionsuppgifter
1. Beskriv hur en rotationsmatris är uppbyggd.
2. Hur åstadkommer du rotation moturs respektive medurs?
 Hämtar...
Hämtar...