4.3 Tillämpningar
SamverkanLinalgLIU
| (3 mellanliggande versioner visas inte.) | |||
| Rad 8: | Rad 8: | ||
<div class="ovning"> | <div class="ovning"> | ||
| - | + | '''''Läs textavsnitt''''' [http://wiki.math.se/wikis/samverkan/linalg-LIU/img_auth.php/1/19/Kap4_3.pdf 4.3 Tillämpningar]. | |
</div> | </div> | ||
| - | + | ||
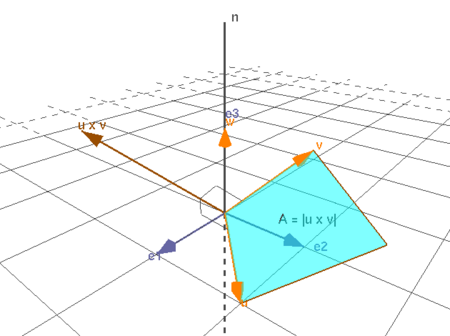
| - | '' | + | '''''Innan du börjar arbeta med detta moment så kan Du utföra beräkning av vektorprodukt genom att klicka på bilden.''''' |
| + | |||
<imagemap> | <imagemap> | ||
| - | Bild:VectorProduct.png| | + | Bild:VectorProduct.png|450px|alt=Alt text |
default [http://webcourses.itn.liu.se/webkurs/VectorProduct.jnlp Du kan här utföra beräkning av vektorprodukt] | default [http://webcourses.itn.liu.se/webkurs/VectorProduct.jnlp Du kan här utföra beräkning av vektorprodukt] | ||
</imagemap> | </imagemap> | ||
| - | </div> | ||
| - | '''''Du har nu läst tillämpningar på vektorprodukt och här kommer några övningar som testar om du har tagit till dig stoffet.''''' | ||
| - | {\color{Blue}hej} | ||
__TOC__ | __TOC__ | ||
Nuvarande version
| 4.1 | 4.2 | 4.3 |
Läs textavsnitt 4.3 Tillämpningar.
Innan du börjar arbeta med detta moment så kan Du utföra beräkning av vektorprodukt genom att klicka på bilden.
Innehåll |
Övning 5.5
Bestäm arean av den triangel som har hörn i \displaystyle (1,1,1) , \displaystyle (1,2,1) och \displaystyle (3,2,1).
Övning 5.6
Bestäm arean för en parallellogram som har hörnpunkterna \displaystyle (1,3,2) , \displaystyle (2,-1,1) , \displaystyle (-1,2,3) och \displaystyle (0,-2,2) .
Övning 5.7
Bestäm arean av en parallellogram som har diagonalvektorerna \displaystyle \boldsymbol{v} =\begin{pmatrix} 2 \\ -5 \\ -3\end{pmatrix} och \displaystyle \boldsymbol{w} = \begin{pmatrix} 4\\ 3\\ -1\end{pmatrix}.
Övning 5.8
Bestäm volymen av den parallellepiped som spänns upp av vektorerna \displaystyle \begin{pmatrix} 3 \\ 1 \\ 7\end{pmatrix},
\displaystyle \begin{pmatrix} 2 \\ -3 \\ 5\end{pmatrix} och \displaystyle \begin{pmatrix} 9 \\ 0 \\ 1\end{pmatrix}.
Övning 5.9
Vilka av följande uppsättningar av vektorer är linjärt beroende?
{\rm a)}\ \begin{pmatrix} 1 \\ 0 \\ 3\end{pmatrix}. \begin{pmatrix} 6 \\ 1 \\ 5\end{pmatrix}. \begin{pmatrix} 8 \\ 1 \\ 11\end{pmatrix} \qquad {\rm b)}\ \begin{pmatrix} 1 \\ 1 \\ 1\end{pmatrix}. \begin{pmatrix} 6 \\ 7 \\ 0\end{pmatrix}. \begin{pmatrix} 1 \\ 2 \\ 3\end{pmatrix}.
Övning 5.10
För vilka \displaystyle a är vektorerna \displaystyle \begin{pmatrix} a \\ 1 \\ 1\end{pmatrix}, \displaystyle \begin{pmatrix} 1 \\ a \\ 2\end{pmatrix} och \displaystyle \begin{pmatrix} 1 \\ 1 \\ a+1\end{pmatrix} linjärt beroende?
Övning 5.11
För vilka \displaystyle t ligger punkterna \displaystyle (t,1,2), \displaystyle (1,t,3), \displaystyle (1,1,1) och \displaystyle (0,1,1) i ett plan?
Övning 5.12
Ange ett värde på talet \displaystyle a så att vektorekvationen
\times \begin{pmatrix} x\\ y \\ z\end{pmatrix} =\begin{pmatrix} 1 \\ a \\ 3\end{pmatrix}
blir lösbar.
Övning 5.13
Antag att \displaystyle \boldsymbol{u} = \begin{pmatrix} 1 \\ -1 \\ 2\end{pmatrix} och \displaystyle \boldsymbol{v} =\begin{pmatrix} -k \\ 1 \\ k\end{pmatrix}. Lös vektorekvationen \displaystyle \boldsymbol{u} \times \boldsymbol{x} = \boldsymbol{v} för alla reella tal \displaystyle k , för vilka ekvationen är lösbar.
Övning 5.14
Låt \displaystyle \boldsymbol{u} = \begin{pmatrix} 1 \\ 1 \\ 2\end{pmatrix} och \displaystyle \boldsymbol{v} = \begin{pmatrix} 2 \\ 1 \\ 1\end{pmatrix}. Bestäm alla lösningar \displaystyle \boldsymbol{x} till ekvationssystemet
\left\{\begin{array}{rcr} \boldsymbol{u} \cdot ( \boldsymbol{x} \times \boldsymbol{v} )&=&0\\ \boldsymbol{u} \cdot \boldsymbol{x} &=&0 \end{array}\right.

 Hämtar...
Hämtar...