20.2 Andragradskurvor

SamverkanLinalgLIU

(Skillnad mellan versioner)
Hoppa till: navigering, sök
Nuvarande version (12 september 2011 kl. 14.41) (redigera) (ogör)
 
(5 mellanliggande versioner visas inte.)
Rad 4: Rad 4:
{{Mall:Vald flik|[[20.2 Andragradskurvor|20.2]]}}
{{Mall:Vald flik|[[20.2 Andragradskurvor|20.2]]}}
{{Mall:Ej vald flik|[[20.3 Andragradsytor|20.3]]}}
{{Mall:Ej vald flik|[[20.3 Andragradsytor|20.3]]}}
-
{{Mall:Ej vald flik|[[20.4 Teckenkaraktär|20.4]]}}
+
{{Mall:Ej vald flik|[[20.4 Teckenkaraktär hos kvadratiska former|20.4]]}}
| style="border-bottom:1px solid #797979" width="100%"|  
| style="border-bottom:1px solid #797979" width="100%"|  
|}
|}
Rad 11: Rad 11:
Läs textavsnitt [http://wiki.math.se/wikis/samverkan/linalg-LIU/img_auth.php/7/7a/Kap20_2.pdf 20.2 Andragradskurvor].
Läs textavsnitt [http://wiki.math.se/wikis/samverkan/linalg-LIU/img_auth.php/7/7a/Kap20_2.pdf 20.2 Andragradskurvor].
-
Du har nu läst om andragradskurvor och här kommer några övningar som testar om du har tagit till dig stoffet.
 
 +
'''''Innan Du börjar arbeta med detta moment så kan Du visualisera andragradskurvor genom att klicka på bilden.'''''
-
===Övning 18.1===
+
<imagemap>
 +
Bild:SecondDegreeCurves.png|450px|alt=Alt text
 +
default [http://webcourses.itn.liu.se/webkurs/SecondDegreeCurves.jnlp Du kan visualisera andragradskurvor]
 +
</imagemap>
 +
 
 +
 
 +
'''''Du kan visualisera andragradskurvor på allmän form genom att klicka på bilden.'''''
 +
 
 +
<imagemap>
 +
Bild:SecDegreeTilted.png|450px|alt=Alt text
 +
default [http://webcourses.itn.liu.se/webkurs/SecDegreeTilted.jnlp Du kan visualisera andragradskurvor på allmän form]
 +
</imagemap>
 +
 
 +
 
 +
 
 +
__TOC__
 +
<div class="ovning">
 +
===Övning 22.23===
 +
Bestäm största och minsta värde av den kvadratiska formen
 +
<center><math>
 +
Q=x_1^2+\sqrt3x_1x_2+2x_2^2
 +
</math></center>
 +
på enhetscirkeln <math> x_1^2+x_2^2=1 </math> och ange i vilka punkter extremvärdena antas.
 +
</div>{{#NAVCONTENT:Svar|Svar till U 22.23|Tips och lösning|Tips och lösning till U 22.23}}
 +
 
 +
 
 +
 
 +
 
 +
<div class="ovning">
 +
===Övning 22.24===
 +
Låt <math> d </math> vara avståndet från en punkt på kurvan
 +
<center><math>
 +
3x_1^2+4x_1x_2=9
 +
</math></center>
 +
till origo. Rita kurvan i ett väl valt koordinatsystem. Vilka värden kan <math> d </math> anta? I förekommande fall ange de
 +
punkter där <math> d </math> antar sitt största respektive minsta värde.
 +
</div>{{#NAVCONTENT:Svar|Svar till U 22.24|Tips och lösning|Tips och lösning till U 22.24}}
 +
 
 +
 
 +
 
 +
 
 +
<div class="ovning">
 +
===Övning 22.25===
 +
Beskriv kurvan
 +
<center><math>
 +
17x_1^2-12x_1x_2+8x_2^2=20.
 +
</math></center>
 +
Ange de punkter på kurvan som ligger närmast respektive längst bort från origo.
 +
</div>{{#NAVCONTENT:Svar|Svar till U 22.25|Tips och lösning|Tips och lösning till U 22.25}}
 +
 
 +
 
 +
 
 +
 
 +
<div class="ovning">
 +
===Övning 22.26===
 +
Visa att andragradskurvan i <math> {\bf R}^2 </math>, definierad av
 +
<center><math>
 +
x_1^2-2x_1x_2+3x_2^2=1
 +
</math></center>
 +
betyder en ellips.
 +
 
 +
Ange också ellipsens area. Det anses känt att ellipsen <math> \frac{x^2_1}{a^2}+\frac{x^2_2}{b^2}=1 </math> har arean <math> \pi ab </math>.
 +
 
 +
Ange de punkter på kurvan som ligger närmast respektive längst bort från origo.
 +
</div>{{#NAVCONTENT:Svar|Svar till U 22.26|Tips och lösning|Tips och lösning till U 22.26}}

Nuvarande version

       20.1          20.2          20.3          20.4      


Läs textavsnitt 20.2 Andragradskurvor.


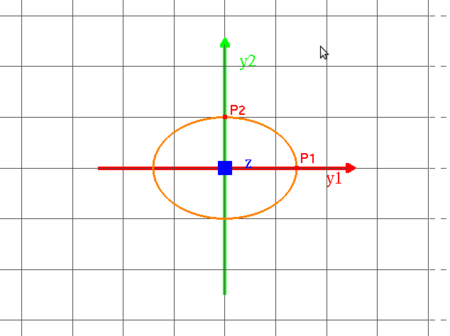
Innan Du börjar arbeta med detta moment så kan Du visualisera andragradskurvor genom att klicka på bilden.

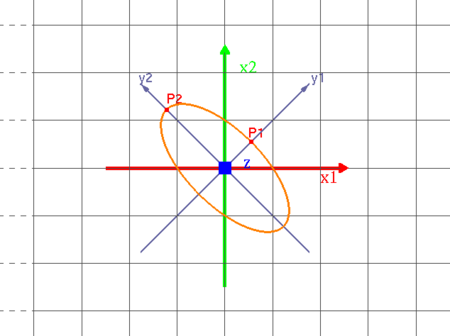
alt=Alt textBildinformation


Du kan visualisera andragradskurvor på allmän form genom att klicka på bilden.

alt=Alt textBildinformation


Innehåll

Övning 22.23

Bestäm största och minsta värde av den kvadratiska formen

\displaystyle

Q=x_1^2+\sqrt3x_1x_2+2x_2^2

på enhetscirkeln \displaystyle x_1^2+x_2^2=1 och ange i vilka punkter extremvärdena antas.

Svar
Svar till U 22.23
Tips och lösning
Tips och lösning till U 22.23



Övning 22.24

Låt \displaystyle d vara avståndet från en punkt på kurvan

\displaystyle

3x_1^2+4x_1x_2=9

till origo. Rita kurvan i ett väl valt koordinatsystem. Vilka värden kan \displaystyle d anta? I förekommande fall ange de punkter där \displaystyle d antar sitt största respektive minsta värde.

Svar
Svar till U 22.24
Tips och lösning
Tips och lösning till U 22.24



Övning 22.25

Beskriv kurvan

\displaystyle

17x_1^2-12x_1x_2+8x_2^2=20.

Ange de punkter på kurvan som ligger närmast respektive längst bort från origo.

Svar
Svar till U 22.25
Tips och lösning
Tips och lösning till U 22.25



Övning 22.26

Visa att andragradskurvan i \displaystyle {\bf R}^2 , definierad av

\displaystyle

x_1^2-2x_1x_2+3x_2^2=1

betyder en ellips.

Ange också ellipsens area. Det anses känt att ellipsen \displaystyle \frac{x^2_1}{a^2}+\frac{x^2_2}{b^2}=1 har arean \displaystyle \pi ab .

Ange de punkter på kurvan som ligger närmast respektive längst bort från origo.

Svar
Svar till U 22.26
Tips och lösning
Tips och lösning till U 22.26
Den här artikeln är hämtad från http://wiki.sommarmatte.se/wikis/samverkan/linalg-LIU/index.php/20.2_Andragradskurvor