SamverkanLinalgLIU

Versionen från 12 september 2011 kl. 13.05 (redigera) Geoba (Diskussion | bidrag) ← Gå till föregående ändring		Nuvarande version (12 september 2011 kl. 14.44) (redigera) (ogör) Geoba (Diskussion | bidrag)
(4 mellanliggande versioner visas inte.)
Rad 17:		Rad 17:
	Läs textavsnitt [http://wiki.math.se/wikis/samverkan/linalg-LIU/img_auth.php/e/ea/Kap16_11.pdf 16.11 Rotationer]		Läs textavsnitt [http://wiki.math.se/wikis/samverkan/linalg-LIU/img_auth.php/e/ea/Kap16_11.pdf 16.11 Rotationer]
		+
	'''''Innan Du börjar arbeta med detta moment så kan Du se en filmvisning om rotation genom att klicka på bilden.'''''		'''''Innan Du börjar arbeta med detta moment så kan Du se en filmvisning om rotation genom att klicka på bilden.'''''
	<imagemap>		<imagemap>
-	Bild:RotationFilm.png|350px|alt=Alt text	+	Bild:RotationFilm.png|450px|alt=Alt text
	default [http://webcourses.itn.liu.se/webkurs/RotationFilm.jnlp Du se en filmvisning om rotation]		default [http://webcourses.itn.liu.se/webkurs/RotationFilm.jnlp Du se en filmvisning om rotation]
	</imagemap>		</imagemap>
Rad 27:		Rad 28:
-	'''''Innan Du börjar arbeta med detta moment så kan Du visualisera rotation genom att klicka på bilden.'''''	+	'''''Du kan visualisera rotation genom att klicka på bilden.'''''
	<imagemap>		<imagemap>
-	Bild:Rotation.png|350px|alt=Alt text	+	Bild:Rotation.png|450px|alt=Alt text
	default [http://webcourses.itn.liu.se/webkurs/Rotation.jnlp Du kan visualisera rotation]		default [http://webcourses.itn.liu.se/webkurs/Rotation.jnlp Du kan visualisera rotation]
	</imagemap>		</imagemap>
Rad 60:		Rad 61:
	Tips och lösning|Tips och lösning till övning 17.38}}		Tips och lösning|Tips och lösning till övning 17.38}}
-	'''''Du har möjlighet att visualisera uppgift 17.38 genom att klicka på länken under bilden.'''''
-	[[Bild:Ex1738a.png|| |350px]]
-
-	[http://webstaff.itn.liu.se/%7Egeoba/TNA002/webkurs/IntersectionSurfaceCylinder.jnlp Starta visualiseringen av uppgift 17.38.]
		+	'''''Du kan visualisera uppgift 17.38 genom att klicka på bilden.'''''
		+	<imagemap>
		+	Bild:Ex1738a.png|450px|alt=Alt text
		+	default [http://webcourses.itn.liu.se/webkurs/Ex1738a.jnlp Du kan visualisera uppgift 17.38]
		+	</imagemap>

---

Nuvarande version

16.1

16.2

16.3

16.4

16.5

16.6

16.7

16.8

16.9

16.10

16.11

Läs textavsnitt 16.11 Rotationer

Innan Du börjar arbeta med detta moment så kan Du se en filmvisning om rotation genom att klicka på bilden.

Du kan visualisera rotation genom att klicka på bilden.

Övningar

17.37 Givet en höger ON-bas i rummet. Följande matriser definierar linjära avbildningar i rummet. Beskriv geometriskt vad dessa gör.

\displaystyle

A_1=\left(\begin{array}{rrr} 1&0 & 0\\ 0& 0& 0\\ 0& 0& 1\end{array}\right)\qquad A_2=\left(\begin{array}{rrr} 1& 0& 0\\ 0& 3& 0\\ 0& 0& 1\end{array}\right)\qquad A_3=\left(\begin{array}{rrr} 1& 0& 0\\ 0& \cos\theta& -\sin\theta\\ 0& \sin\theta& \cos\theta\end{array}\right)

17.38 Låt \displaystyle \underline{\boldsymbol{e}} vara en höger ON-bas i rummet och låt en rotationsaxel \displaystyle L vara parallell med vektorn \displaystyle 2\boldsymbol{e}_1+2\boldsymbol{e}_2-\boldsymbol{e}_3.

1. Bestäm \displaystyle F:s matris \displaystyle A_{\boldsymbol{e}} om \displaystyle F är en rotation \displaystyle \pi/2 i positiv led runt \displaystyle L.
2. Bestäm \displaystyle G:s matris \displaystyle B_{\boldsymbol{e}} om \displaystyle G är en rotation \displaystyle 3\pi/2 i positiv led runt \displaystyle L.
3. Bestäm \displaystyle A^4_{\boldsymbol{e}}.

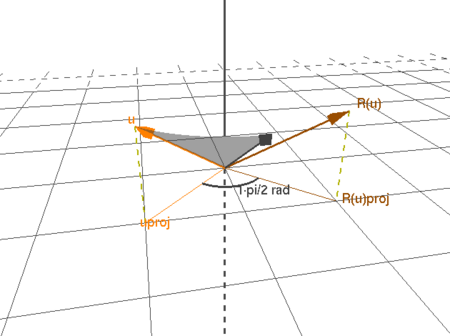
Du kan visualisera uppgift 17.38 genom att klicka på bilden.

17.39. Låt \displaystyle \underline{\boldsymbol{e}} vara en höger ON-bas i rummet och \displaystyle F rotation \displaystyle 2\pi/3 i positiv led runt \displaystyle \boldsymbol{e}_1+\boldsymbol{e}_2+\boldsymbol{e}_3. Beräkna avbildningens matris i basen \displaystyle \underline{\boldsymbol{e}}.

Reflektionsuppgifter

1. Beskriv hur en rotationsmatris är uppbyggd.

2. Hur åstadkommer du rotation moturs respektive medurs?