Förberedande kurs i matematik

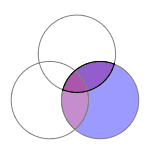
Vi letar efter mängden som är markerad med blå färg i Venn-diagrammet. Vi vill alltså veta hur många element det finns i

\displaystyle \qquad C/A/B

Tyvärr så gäller det inte att

\displaystyle \qquad |C/A/B|=|C|-|A|-|B|

Svaret skulle ju bli negativt med ovanstående formel! Detta beror på att vi har tagit bort element som ligger i \displaystyle A och \displaystyle B, men inte i \displaystyle C. Istället ska vi dra bort \displaystyle A\cap C och \displaystyle B\cap C från \displaystyle C. Tyvärr är inte problemet så enkelt heller.

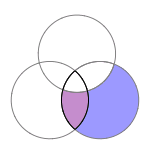
Vi börjar alltså med mängden av elever som gillar matematik: \displaystyle C. Vi vet att det finns \displaystyle 12 sådana elever. Vi är inte intresserade av sådana elever som även gillar fysik, dvs. mängden \displaystyle A\cap C. Enligt uppgiften så har vi \displaystyle |A\cap C|=8. Mängden \displaystyle A\cap C markerad med svart i diagrammet nedan:

Vi vill alltså bli av med sådana element som ligger både i \displaystyle A och \displaystyle C:

\displaystyle \qquad |C|-|A\cap C| = 12-8 = 4

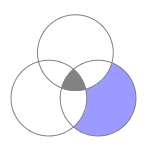
Vi är inte heller intresserade av elever som tycker om både matematik och biologi. Denna mängd betecknas med \displaystyle B\cap C och enligt uppgiften har vi att \displaystyle |B\cap C|=5. Området är markerad med svart nedan:

Men om vi nu drar bort \displaystyle |B\cap C| ur det vi fick förut så får vi att

\displaystyle \qquad |C|-|A\cap C|-|B\cap C| = 4-5 = -1

Ett negativt tal alltså! Men det är väl inte rimligt? Vad har vi gjort fel? Jo, vi har faktiskt dragit bort \displaystyle |A\cap B\cap C| två gånger!

Alltså måste vi lägga till \displaystyle |A\cap B\cap C| en gång för att balansera våra beräkningar. Enligt uppgiften har vi att \displaystyle |A\cap B\cap C|=1varav följer att

\displaystyle \qquad |C/A/B|=|C|-|A\cap C|-|B\cap C| + |A\cap B\cap C|= 12-8-5+1 = 0

Alltså finns det inga elever som enbart tycker om matematik.