Testsida3
Förberedande kurs i matematik
Innehåll |
Övning 2.3.4
Övning 2.3.2
| a) Hur många palidromer av längd 6 kan man bilda med hjälp av siffrorna \displaystyle 0,1,2,\dots,9? |
| b) Hur många palidromer av längd 5 kan man bilda med hjälp av siffrorna \displaystyle 0,1,2,\dots,9? |
Övning 2.3.3
|
Man kan välja mellan 3 olika tröjor (röd, gul och svart), 2 olika byxor (vita och svarta) och 5 olika hattar (gul, vit, svart, grön och blå). |
| a) Lena är inte så stilig, hon kombinerar färger fritt. På hur många sätt kan hon välja sina kläder? |
| b) Jonas vill ha svarta byxor och en gul tröja, men hattens färg tycker han inte är så viktig. Hur många olika klädval har han? |
| c) Anna vill inte kombinera svarta byxor med en gul tröja. På hur många sätt kan hon kombinera olika kläder? |
Övning 4....
Låt \displaystyle f(x)=\sqrt{x}. Vilka av följande val till definitions- och målmängd är tillåtna?
| a) \displaystyle f:\mathbb{R}_+\to \mathbb{R}_+ |
| b) \displaystyle f:\mathbb{R}_+\to \mathbb{R} |
| c) \displaystyle f:\mathbb{R}\to \mathbb{R} |
| d) \displaystyle f:\mathbb{R}\to \mathbb{C} |
| e) \displaystyle f:\mathbb{C}\to \mathbb{C} |
Övning 4.2.2
En punkt kallas \displaystyle a ett lokalt minimum om funktionsvärdena precis intill punkten är mindre än eller lika med \displaystyle f(a). På motsvarande sätt definieras ett lokalt maximum. Hitta antalet lokala maximi- och minimipunkter på intervallet \displaystyle (-2,2). Notera att \displaystyle 2 och \displaystyle -2 inte ligger på intervallet.
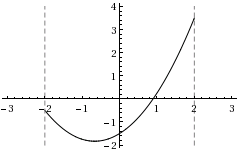
| a) | \displaystyle f(x)=\frac{3x^2}{4} +x-3/2 | |
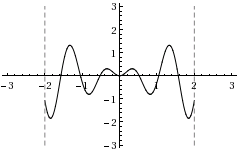
| b) | \displaystyle f(x)=x\sin{(6x)} | |
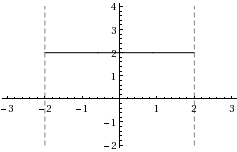
| c) | \displaystyle f(x)=2 | |
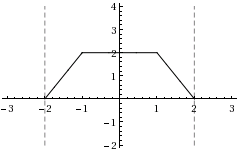
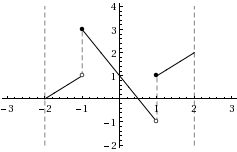
| d) | \displaystyle f(x)=\begin{cases}-2x+4&\text{om }x<-1\\2&\text{om }-1\leq x\leq 1\\2x+4&\text{om }x>1\end{cases} | |
| e) | \displaystyle f(x)=x+1 | |
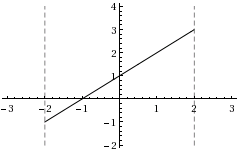
| f) | \displaystyle f(x)=\begin{cases}x+2&\text{om }x<-1\\-2 x + 1&\text{om }-1\leq x< 1\\x&\text{om }x\geq 1\end{cases} |
 Hämtar...
Hämtar...