Testsida3
Förberedande kurs i matematik
(Skillnad mellan versioner)
| Rad 19: | Rad 19: | ||
|- | |- | ||
|f) | |f) | ||
| - | |[[Bild:Kap4plotF.png|left]]<math>f(x)=\begin{cases} | + | |[[Bild:Kap4plotF.png|left]]<math>f(x)=\begin{cases}x+2&\text{om }x<-1\\-2 x + 1&\text{om }-1\leq x< 1\\x&\text{om }x\geq 1\end{cases}</math> |
|| | || | ||
|} | |} | ||
</div>{{#NAVCONTENT:Svar| Svar 4.2.2 | Lösning 4.2.2 a | Lösning 4.4.2.a }} | </div>{{#NAVCONTENT:Svar| Svar 4.2.2 | Lösning 4.2.2 a | Lösning 4.4.2.a }} | ||
Versionen från 19 juni 2012 kl. 14.30
Övning 4.2.2
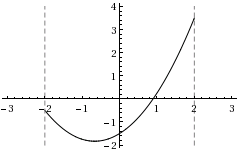
| a) | \displaystyle f(x)=\frac{3x^2}{4} +x-3/2 | |
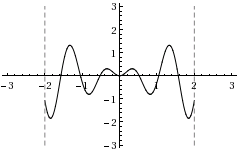
| b) | \displaystyle f(x)=x\sin{(6x)} | |
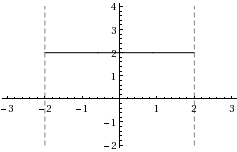
| c) | \displaystyle f(x)=2 | |
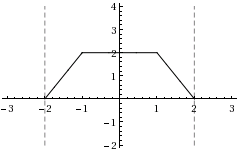
| d) | \displaystyle f(x)=\begin{cases}-2x+4&\text{om }x<-1\\2&\text{om }-1\leq x\leq 1\\2x+4&\text{om }x>1\end{cases} | |
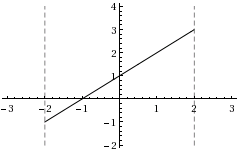
| e) | \displaystyle f(x)=x+1 | |
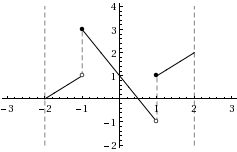
| f) | \displaystyle f(x)=\begin{cases}x+2&\text{om }x<-1\\-2 x + 1&\text{om }-1\leq x< 1\\x&\text{om }x\geq 1\end{cases} |
Svar
Lösning 4.2.2 a
 Hämtar...
Hämtar...