Processing Math: Done
To print higher-resolution math symbols, click the
Hi-Res Fonts for Printing button on the jsMath control panel.
No jsMath TeX fonts found -- using image fonts instead.
These may be slow and might not print well.
Use the jsMath control panel to get additional information.
jsMath Control PanelHide this Message

jsMath

Lösning 2.5.1b

Förberedande kurs i matematik

(Skillnad mellan versioner)
Hoppa till: navigering, sök
(Ny sida: rightEnligt sambandet <math>\cos(x)=\cos(-x)</math> är <math>\qquad -\frac{5\pi}{6}</math> också en lösning. Denna vinkel ligger på intervallet <math>(-\pi...)
Nuvarande version (2 augusti 2012 kl. 12.43) (redigera) (ogör)
 
Rad 1: Rad 1:
-
[[Bild:Övning251_cos.png|right]]Enligt sambandet <math>\cos(x)=\cos(-x)</math> är
+
[[Bild:Övning251_cos.png|right]]I deluppgift a) såg vi att <math>5\pi/6</math> är en lösning till ekvationen. Enligt sambandet <math>\cos(x)=\cos(-x)</math> måste
<math>\qquad -\frac{5\pi}{6}</math>
<math>\qquad -\frac{5\pi}{6}</math>
-
också en lösning. Denna vinkel ligger på intervallet <math>(-\pi,\pi]</math>.
+
också vara en lösning. Denna vinkel ligger på intervallet <math>(-\pi,\pi]</math>.
-
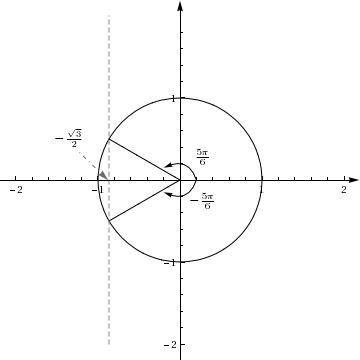
Om vi ritar upp enhetscirkeln och markerar vinklarna <math>\frac{5\pi}{6}</math> och <math>-\frac{5\pi}{6}</math> där så ser vi att det inte finns andra vinklar på intervallet <math>(-\pi,\pi]</math> vars cos-värde skulle vara lika med <math>-\sqrt{3}/2</math> (kom ihåg att cos motsvarar <math>x</math>-koordinaten).
+
Om vi ritar upp enhetscirkeln och markerar vinklarna <math>\frac{5\pi}{6}</math> och <math>-\frac{5\pi}{6}</math> där så ser vi att det inte finns andra vinklar på intervallet <math>(-\pi,\pi]</math> vars cos-värde skulle vara lika med <math>-\sqrt{3}/2</math> (kom ihåg att cos motsvarar <math>x</math>-koordinaten). När man löser trigonometriska uppgifter är det alltid bra att rita upp enhetscirkeln: på så sätt är det lätt att kontrollera att man inte har missat några lösningar!

Nuvarande version

I deluppgift a) såg vi att 56 är en lösning till ekvationen. Enligt sambandet cos(x)=cos(−x) måste

−65

också vara en lösning. Denna vinkel ligger på intervallet (−].

Om vi ritar upp enhetscirkeln och markerar vinklarna 65 och −65 där så ser vi att det inte finns andra vinklar på intervallet (−] vars cos-värde skulle vara lika med −32  (kom ihåg att cos motsvarar x-koordinaten). När man löser trigonometriska uppgifter är det alltid bra att rita upp enhetscirkeln: på så sätt är det lätt att kontrollera att man inte har missat några lösningar!

Den här artikeln är hämtad från http://wiki.sommarmatte.se/wikis/forberedandematte/index.php/L%C3%B6sning_2.5.1b