Att skriva lösningar

Förberedande kurs i matematik

(Skillnad mellan versioner)
Hoppa till: navigering, sök
Nuvarande version (12 augusti 2012 kl. 17.52) (redigera) (ogör)
 
(11 mellanliggande versioner visas inte.)
Rad 1: Rad 1:
 +
===Inlämningsuppgifter===
 +
 +
[[Bild:Inlämningsuppgifter.png | right | Student Lounge]]
 +
På inlämningsuppgifterna ska du skriva lösningar, '''där du inte bara skriver ned ett svar utan även förklarar vad du gjort och varför'''.
 +
 +
Lösningen rättas normalt inom en vardag, men ibland kan rättningen ta två till tre vardagar. Under sommaren rättas inlämningsuppgifterna under helger också. Lösningen behöver inte vara perfekt första gången - efter att uppgiften rättats, kommer du ha möjlighet att komplettera den om det behövs. Du får hur många försök på dig som du behöver, men var noga även när du kompletterar - det är inte kul att behöva vänta flera dagar på att få en uppgift godkänd, bara för att man gjort några slarvfel eller inte skrivit en läsbar lösning.
 +
 +
----
----
-
På inlämningsuppgifterna ska du skriva lösningar, där du inte bara skriver ned ett svar utan även förklarar vad du gjort och varför. Det viktigaste med en lösning är att vi mentorer ska kunna se att du har de kunskaper som efterfrågas - därför är det väldigt viktigt att du är tydlig med '''vad du gör''' när du löser uppgiften, och att du tydligt '''motiverar''' varför du gjort sakerna.
+
===Vad krävs för att bli godkänd?===
-
Därför räcker det oftast inte att du bara skriver ned ekvationer - det behövs förklarande text också.
+
Det viktigaste med en lösning är att mentorerna ska kunna se att du har de kunskaper som efterfrågas - därför är det väldigt viktigt att du är tydlig med '''vad du gör''' när du löser uppgiften, och att du tydligt '''motiverar''' varför du gjort sakerna.
-
Lösningen rättas oftast normalt inom två vardagar, men ibland kan rättningen även ske under helger. Lösningen behöver inte vara perfekt första gången - efter att uppgiften rättats, kommer du ha möjlighet att komplettera den om det behövs. Du får hur många försök på dig som du behöver för att då uppgiften färdig, men det var noga även när du kompletterar - det är inte kul att behöva vänta flera dagar på att få en uppgift godkänd, bara för att man gjort några slarvfel.
+
Därför räcker det oftast inte att du bara skriver ned ekvationer - det behövs förklarande text också.
-
<div class="inforuta" style="width:580px;background-color:#e4e2e3">
+
Det är enklast om du skriver dina lösningar som klartext direkt i svarsrutan. Eftersom det är många olika personer som rättar uppgifter '''accepterar vi inga svar som skickas via e-post'''.
 +
 
 +
<div class="inforuta" style="width:580px;background-color:#afcae5">
 +
'''När du skriver din lösning, kom ihåg att'''
 +
* ange vilken metod du använder,
 +
* förklara svårare steg i lite mer detalj,
 +
* tala om vilka formler du använder,
 +
* svara på alla delfrågor,
 +
* motivera dina svar,
 +
* läsa genom det du skrivit innan du lämnar in och
 +
* skriva tydligt!
 +
 
 +
Du måste beskriva vad du gör! '''Lösningar som består av enbart formler godkänns inte!'''
 +
</div>
 +
 
 +
 
 +
----
 +
 
 +
 
 +
===Samarbete med andra studenter===
 +
 
 +
Det är tillåtet att samarbeta med andra studenter när man löser uppgifter, däremot är det inte tillåtet att skriva lösningarna tillsammans. '''Indentiska lösningar godkänns ej'''.
 +
 
 +
 
 +
----
 +
 
 +
 
 +
===Att komplettera===
 +
 
 +
De flesta blir inte godkända på första försöket. Du får komplettera din lösning så många gånger det behövs.
 +
 
 +
<div class="inforuta" style="width:560px;background-color:#afcae5">
'''Att tänka på när du kompletterar'''
'''Att tänka på när du kompletterar'''
-
Markera tydligt var kompletteringen börjar (alternativt skriv en helt ny lösning). Vi rekommenderar att du inte tar bort rättningskommentarer eftersom om du gör samma fel när du kompletterar är det möjligt att du får exakt samma rättningskommentar tillbaka.
+
'''Markera tydligt''' var kompletteringen börjar, alternativt skriv en helt ny lösning. Annars kan det se ut som att du ger två olika svar på samma fråga.
 +
 
 +
Vi rekommenderar att du '''inte tar bort rättningskommentarer''' eftersom om du gör samma fel igen när du kompletterar är det möjligt att du får exakt samma rättningskommentar tillbaka.
Innan du kompletterar rekommenderar vi att du '''repeterar''' teorin.
Innan du kompletterar rekommenderar vi att du '''repeterar''' teorin.
 +
 +
Glömt inte att motivera dina svar när du kompletterar.
 +
 +
Om du inte förstår rättningskommentarer, fråga för mer detaljerade instruktioner istället av att lämna in samma lösning igen.
</div>
</div>
-
Nedan har vi listat de vanligaste skälen för att bli underkänd på en inlämningsuppgift.
 
-
<ol>
+
----
-
<li>'''Slarvfel.''' Innan du lämnar in din lösning, kontrollera dina beräkningar.</li>
+
 
-
<li>'''Ingen förklarande text.''' Även om det känns onödigt är det bra att förklara det du gör med ord. Då är det lättare för mentorerna att bedöma om du verkligen har förstått problemet. Om du använder en metod som inte finns i kompendiet måste du ''med egna ord'' beskriva hur metoden funkar.
+
 
-
<br/><br/>Följande saken ska framgå av din lösning:
+
===De vanligaste misstagen===
-
* Vilken metod du använder.
+
 
-
* Förklara svårare steg.
+
'''Inlämningsuppgift 2'''
-
* Tala om vilka formler du använder.
+
* Kvadratkomplettering:
-
* I slutet ska du peka ut svaret. Läsaren ska inte behöva läsa genom lösningen för att se svaret.
+
** Ingen förklarande text.
-
<br/><br/>'''Exempel.'''
+
** Studenten kontrollerar inte svaret genom insättning, alternativt konstaterar bara att "svaret stämmer".
-
<br/>''Fråga:'' Hitta alla lösningar till ekvationen <math>x^2+2x-1=0</math>
+
** Studenten använder pq-formeln istället av kvadratkomplettering.
-
[[Bild:ExempelLösning.png]]
+
* Rationella rötter:
-
</li>
+
** Studenten konstaterar att de potentiella rötterna inte löser ekvationen men visar inte beräkningarna.
-
<li>'''Inga beräkningar.''' Det är viktigt att förklara hur man löser en uppgift, men du måste också utföra alla beräkningar du beskriver.</li>
+
'''Inlämningsuppgift 3.1'''
-
<li>'''Använt definition som motivering.''' Att kopiera över en definition från kompendiet och använda det som motivering är inte tillräckligt.
+
* Studenten förstår inte vad som menas med definitions- och målmängd.
-
<br/><br/>'''Exempel.'''
+
* Kopierar över definitionen av en injektiv funktion och använder det som bevis.
-
<br/>''Definition:'' Ett tal är rationellt om det kan skrivas på formen <math>a/b</math> där <math>a</math> och <math>b\neq0</math> är heltal.
+
'''Inlämningsuppgift 3.2'''
-
<br/>''Fråga:'' Är <math>3,05</math> ett rationellt tal?
+
* Pekar inte ut felen.
-
<br/>''Dåligt svar:'' Ja, eftersom <math>3,05</math> kan skrivas på formen <math>a/b</math> där <math>a</math> och <math>b\neq0</math> är heltal.
+
* Ingen förklarande text.
-
<br/>''Bra svar:'' Ett tal är rationellt om det kan skrivas på formen <math>a/b</math> där <math>a</math> och <math>b\neq0</math> är heltal. Talet <math>3,05</math> är rationellt eftersom vi kan skriva <math>3,05=a/b</math> om vi väljer <math>a=305</math> och <math>b=100</math>.
+
'''Inlämningsuppgift 4.1'''
-
</li>
+
* a), b) och c): Inga ord, bara formler
-
<li>'''Inte motiverat/svarat på alla delfrågor.''' Du måste svara på alla frågor som uppgiften innehåller. Dessutom måste du motivera dina svar.</li>
+
* d): Inga formler, bara ord
-
<li>'''Kompletterat på ett otydligt sätt.''' När du kompletterar, markera tydligt var kompletteringen börjar. Alternativt kan du ta bort ditt tidigare svar och skriva en helt ny lösning.
+
* d): Studenten behandlar inte det allmänna fallet utan tar ett exempel. Vanligtvis <math>n=3</math>.
-
<br/><br/>'''Exempel.'''
+
'''Inlämningsuppgift 4.2'''
-
<br/>''Fråga:'' Hur många rötter har polynomet <math>f(x)=x^2+1</math>?
+
* Slarvfel i e)
-
<br/>''Svar 1:'' Vi har <math>f(x)=x^2+1=0</math> vilket är ekvivalent med att <math>x^2=-1</math>. Denna ekvation är omöjlig eftersom ett tal gånger sig själv är aldrig negativt. Alltså saknar polynomet rötter.
+
* Svarar inte på sista frågan i e).
-
<br/>''Rättningskommentar 1:'' Kan det inte finnas komplexa rötter?
+
'''Inlämningsuppgift 5'''
-
<br/>''Svar 2:'' Vi har <math>f(x)=x^2+1=0</math> vilket är ekvivalent med att <math>x^2=-1</math>. Denna ekvation är omöjlig eftersom ett tal gånger sig själv är aldrig negativt. Alltså saknar polynomet rötter. Ekvationen <math>x^2=-1</math> har lösningarna <math>x=\pm i</math>. Alltså har polynomet två rötter.
+
* Decimalutvecklingar och talrepresentation:
-
<br/>''Rättningskommentar 2:'' Du ger ju två olika svar på frågan!
+
** Fråga 3: Studenten tar ett exempel istället av att behandla det allmänna fallet.
-
</li>
+
** Fråga 4-6: Studenten redovisat enbart svaret, ingen förklarande text eller beräkningar.
-
</ol>
+
* Euklides algoritm och Diofantiska ekvationer:
 +
** Slarvfel
 +
** Ingen förklarande text
 +
* Kombinatorik:
 +
** Fråga 2: Det kombinatoriska beviset består av några stycken ofullständiga satser, alternativt av en enda tioraders sats. Studenten kopierar över ledtrådet och sedan pratar om något helt annat.
 +
 
 +
 
 +
----
 +
 
 +
 
 +
===Några exempel på bra och dåliga lösningar===
 +
 
 +
En bra lösning består inte enbart av formler. Även om det känns onödigt är det bra att förklara det du gör med ord. Då är det lättare för mentorerna att bedöma om du verkligen har förstått problemet. Om du använder en metod som inte finns i kompendiet måste du ''med egna ord'' beskriva hur metoden funkar.
 +
 
 +
Det är viktigt att förklara hur man löser en uppgift, men du måste också utföra och redovisa alla beräkningar du beskriver!
 +
 
 +
<div class="exempel">
 +
'''Exempel 1''' (Ingen förklarande text)
 +
 
 +
''Uppgift:'' Hitta alla lösningar till ekvationen <math>x^2+2x-1=0</math>.
 +
 
 +
<div style="width:100%;">
 +
<div style="width:540px; margin-left:auto; margin-right:auto;">
 +
<div style="width:220px;height:280px;float:left;border:1px solid gray;padding:10px;margin:10px">
 +
En dålig lösning:
 +
 
 +
----
 +
 
 +
 
 +
x^2 + 2x - 1 = 0
 +
 
 +
x = -2/2 ± sqrt[(2/2)^2-(-1)]
 +
 
 +
x = -1 ± sqrt(2)
 +
 
 +
Svar:
 +
 
 +
x1 = -1+sqrt(2)
 +
 
 +
x2 = -1-sqrt(2)
 +
</div>
 +
<div style="width:220px;height:280px;float:right;border:1px solid gray;padding:10px;margin:10px">
 +
En bra lösning:
 +
 
 +
----
 +
 
 +
 
 +
Jag använder pq-formeln för att lösa uppgiften. Insättning i pq-formeln ger
 +
 
 +
x = -2/2 ± sqrt[(2/2)^2-(-1)]
 +
 
 +
vilket förkortas till
 +
 
 +
x = -1 ± sqrt(2)
 +
 
 +
Alltså har ekvationen två rötter, x=-1+sqrt(2) samt x=-1-sqrt(2).
 +
</div>
 +
<div style="clear:both"></div>
 +
</div>
 +
 
 +
</div>
 +
Vilken av ovanstående lösningar tycker du är lättare att hänga med?
 +
</div>
 +
 
 +
 
 +
Att kopiera över en definition från kompendiet och använda det som motivering är inte tillräckligt. Du måste också med egna ord förklara varför definitionen är uppfylld.
 +
 
 +
<div class="exempel">
 +
'''Exempel 2''' (Definition som motivering)
 +
 
 +
''Definition:'' Ett tal är rationellt om det kan skrivas på formen <math>a/b</math> där <math>a</math> och <math>b\neq0</math> är heltal.
 +
 
 +
''Uppgift:'' Är <math>3,05</math> ett rationellt tal?
 +
 
 +
<div style="width:100%;">
 +
<div style="width:540px; margin-left:auto; margin-right:auto;">
 +
<div style="width:220px;height:200px;float:left;border:1px solid gray;padding:10px;margin:10px">
 +
Ett dåligt svar:
 +
 
 +
----
 +
 
 +
 
 +
Ja, eftersom 3,05 kan skrivas på formen a/b där a och b är heltal.
 +
</div>
 +
<div style="width:220px;height:200px;float:right;border:1px solid gray;padding:10px;margin:10px">
 +
Ett bra svar:
 +
 
 +
----
 +
 
 +
 
 +
Ett tal är rationellt om det kan skrivas på formen a/b, där a och b är heltal. Vi kan skriva 3,05=a/b om vi väljer a=305 och b=100. Alltså är 3,05 rationellt.
 +
</div>
 +
<div style="clear:both"></div>
 +
</div>
 +
 
 +
</div>
 +
 
 +
 
 +
</div>
 +
 
 +
När du kompletterar, markera tydligt var kompletteringen börjar. Alternativt kan du ta bort ditt tidigare svar och skriva en helt ny lösning. Det händer ofta att man skriver sin nya lösning direkt efter den gamla så att det blir svårt för mentorerna att bedöma om studenten verkligen har förstått.
 +
 
 +
<div class="exempel">
 +
'''Exempel 3''' (Otydlig komplettering)
 +
 
 +
''Uppgift:'' Hur många rötter har polynomet <math>f(x)=x^2+1</math>?
 +
 
 +
<div style="width:100%;">
 +
<div style="width:540px; margin-left:auto; margin-right:auto;">
 +
<div style="width:220px;height:250px;float:left;border:1px solid gray;padding:10px;margin:10px">
 +
Lösning 1:
 +
 
 +
----
 +
 
 +
 
 +
Vi har f(x)=x^2+1=0 vilket är ekvivalent med x^2=-1. Ett tal gånger sig själv kan aldrig vara negativt, alltså saknar polynomet rötter.
 +
</div>
 +
<div style="width:220px;height:250px;float:right;border:1px solid gray;padding:10px;margin:10px">
 +
Rättning 1:
 +
 
 +
----
 +
 
 +
 
 +
Kan det inte finnas komplexa rötter?
 +
 
 +
/mentorerna
 +
 
 +
---
 +
 
 +
Vi har f(x)=x^2+1=0 vilket är ekvivalent med x^2=-1. Ett tal gånger sig själv kan aldrig vara negativt, alltså saknar polynomet rötter.
 +
</div>
 +
<div style="clear:both"></div>
 +
<div style="width:220px;height:300px;float:left;border:1px solid gray;padding:10px;margin:10px">
 +
Lösning 2:
 +
 
 +
----
 +
 
 +
 
 +
Vi har f(x)=x^2+1=0 vilket är ekvivalent med x^2=-1. Ett tal gånger sig själv kan aldrig vara negativt, alltså saknar polynomet rötter. Ekvationen x^2=-1 har lösningarna x=+/-i, alltså har polynomet två rötter.
 +
</div>
 +
<div style="width:220px;height:300px;float:right;border:1px solid gray;padding:10px;margin:10px">
 +
Rättning 2:
 +
 
 +
----
 +
 
 +
 
 +
Du ger ju två olika svar på frågan!
 +
 
 +
/mentorerna
 +
 
 +
---
 +
 
 +
Vi har f(x)=x^2+1=0 vilket är ekvivalent med x^2=-1. Ett tal gånger sig själv kan aldrig vara negativt, alltså saknar polynomet rötter. Ekvationen x^2=-1 har lösningarna x=+/-i, alltså har polynomet två rötter.
 +
</div>
 +
<div style="clear:both"></div>
 +
</div>
 +
 
 +
</div>
 +
 
 +
 
 +
</div>
 +
 
 +
 
 +
----
 +
 
 +
 
 +
===Att vara systematisk===
 +
Vi rekommenderar att du läser igenom de avsnitt i kompendiet som inlämningsuppgiften behandlar. Att försöka lösa inlämningsuppgifterna utan att läsa teori funkar oftast inte. Innan du lämnar in något, läs genom din lösning. För att bli godkänd måste du ha svarat på alla delfrågor och motiverat dina svar. Kom ihåg att vara tydlig!
 +
 
 +
Här hittar du en lista över viktiga avsnitt:
 +
 
 +
* '''Inlämningsuppgift 2:''' Avsnitt 2.1-2.2. Se även inspelningen av Lektion 3.
 +
* '''Inlämningsuppgift 3.1:''' Avsnitt 3.1-3.2. Se även inspelningen av Lektion 5 samt extra [[Övningar_Kapitel_3 | övningsuppgifter]] till avsnitt 3.2.
 +
* '''Inlämningsuppgift 3.2:''' Avsnitt 3.3-3.4. Se även inspelningen av Lektion 5 och 6.
 +
* '''Inlämningsuppgift 4.1:''' Avsnitt 4.1-4.2. Se även inspelningen av Lektion 7.
 +
* '''Inlämningsuppgift 4.2:''' Avsnitt 4.3. Se även inspelningen av Lektion 8.
 +
* '''Inlämningsuppgift 5:''' Specialiseringstexten (se [[Kurslitteratur]])
 +
 
 +
Ni förväntas även känna till de tidigare avsnitten! För ett mer detaljerat dagsschema, se [[Studieplan]].
 +
 
 +
 
 +
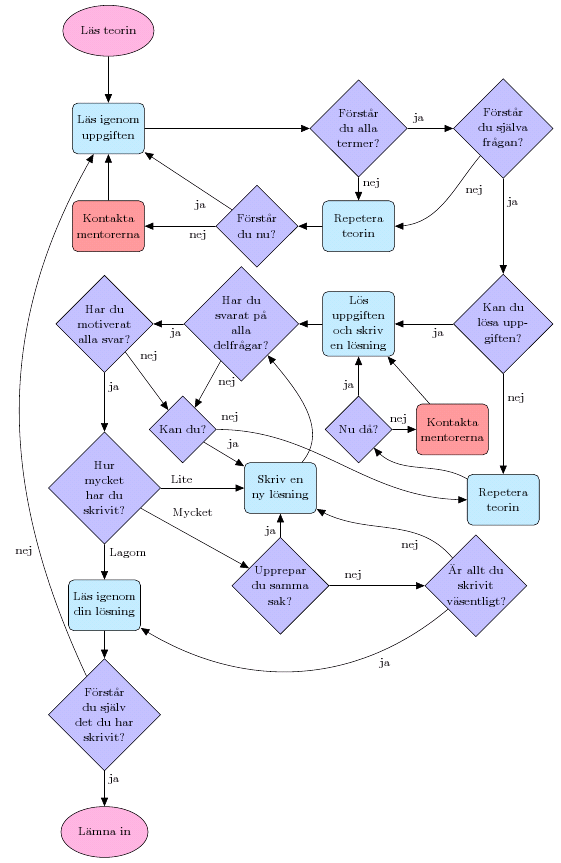
[[Bild:Flowchart.png | center | Att lösa inlämningsuppgifter]]
 +
 
 +
 
----
----

Nuvarande version

Innehåll

Inlämningsuppgifter

Student Lounge

På inlämningsuppgifterna ska du skriva lösningar, där du inte bara skriver ned ett svar utan även förklarar vad du gjort och varför.

Lösningen rättas normalt inom en vardag, men ibland kan rättningen ta två till tre vardagar. Under sommaren rättas inlämningsuppgifterna under helger också. Lösningen behöver inte vara perfekt första gången - efter att uppgiften rättats, kommer du ha möjlighet att komplettera den om det behövs. Du får hur många försök på dig som du behöver, men var noga även när du kompletterar - det är inte kul att behöva vänta flera dagar på att få en uppgift godkänd, bara för att man gjort några slarvfel eller inte skrivit en läsbar lösning.



Vad krävs för att bli godkänd?

Det viktigaste med en lösning är att mentorerna ska kunna se att du har de kunskaper som efterfrågas - därför är det väldigt viktigt att du är tydlig med vad du gör när du löser uppgiften, och att du tydligt motiverar varför du gjort sakerna.

Därför räcker det oftast inte att du bara skriver ned ekvationer - det behövs förklarande text också.

Det är enklast om du skriver dina lösningar som klartext direkt i svarsrutan. Eftersom det är många olika personer som rättar uppgifter accepterar vi inga svar som skickas via e-post.

När du skriver din lösning, kom ihåg att

  • ange vilken metod du använder,
  • förklara svårare steg i lite mer detalj,
  • tala om vilka formler du använder,
  • svara på alla delfrågor,
  • motivera dina svar,
  • läsa genom det du skrivit innan du lämnar in och
  • skriva tydligt!

Du måste beskriva vad du gör! Lösningar som består av enbart formler godkänns inte!



Samarbete med andra studenter

Det är tillåtet att samarbeta med andra studenter när man löser uppgifter, däremot är det inte tillåtet att skriva lösningarna tillsammans. Indentiska lösningar godkänns ej.



Att komplettera

De flesta blir inte godkända på första försöket. Du får komplettera din lösning så många gånger det behövs.

Att tänka på när du kompletterar

Markera tydligt var kompletteringen börjar, alternativt skriv en helt ny lösning. Annars kan det se ut som att du ger två olika svar på samma fråga.

Vi rekommenderar att du inte tar bort rättningskommentarer eftersom om du gör samma fel igen när du kompletterar är det möjligt att du får exakt samma rättningskommentar tillbaka.

Innan du kompletterar rekommenderar vi att du repeterar teorin.

Glömt inte att motivera dina svar när du kompletterar.

Om du inte förstår rättningskommentarer, fråga för mer detaljerade instruktioner istället av att lämna in samma lösning igen.



De vanligaste misstagen

Inlämningsuppgift 2

  • Kvadratkomplettering:
    • Ingen förklarande text.
    • Studenten kontrollerar inte svaret genom insättning, alternativt konstaterar bara att "svaret stämmer".
    • Studenten använder pq-formeln istället av kvadratkomplettering.
  • Rationella rötter:
    • Studenten konstaterar att de potentiella rötterna inte löser ekvationen men visar inte beräkningarna.

Inlämningsuppgift 3.1

  • Studenten förstår inte vad som menas med definitions- och målmängd.
  • Kopierar över definitionen av en injektiv funktion och använder det som bevis.

Inlämningsuppgift 3.2

  • Pekar inte ut felen.
  • Ingen förklarande text.

Inlämningsuppgift 4.1

  • a), b) och c): Inga ord, bara formler
  • d): Inga formler, bara ord
  • d): Studenten behandlar inte det allmänna fallet utan tar ett exempel. Vanligtvis \displaystyle n=3.

Inlämningsuppgift 4.2

  • Slarvfel i e)
  • Svarar inte på sista frågan i e).

Inlämningsuppgift 5

  • Decimalutvecklingar och talrepresentation:
    • Fråga 3: Studenten tar ett exempel istället av att behandla det allmänna fallet.
    • Fråga 4-6: Studenten redovisat enbart svaret, ingen förklarande text eller beräkningar.
  • Euklides algoritm och Diofantiska ekvationer:
    • Slarvfel
    • Ingen förklarande text
  • Kombinatorik:
    • Fråga 2: Det kombinatoriska beviset består av några stycken ofullständiga satser, alternativt av en enda tioraders sats. Studenten kopierar över ledtrådet och sedan pratar om något helt annat.



Några exempel på bra och dåliga lösningar

En bra lösning består inte enbart av formler. Även om det känns onödigt är det bra att förklara det du gör med ord. Då är det lättare för mentorerna att bedöma om du verkligen har förstått problemet. Om du använder en metod som inte finns i kompendiet måste du med egna ord beskriva hur metoden funkar.

Det är viktigt att förklara hur man löser en uppgift, men du måste också utföra och redovisa alla beräkningar du beskriver!

Exempel 1 (Ingen förklarande text)

Uppgift: Hitta alla lösningar till ekvationen \displaystyle x^2+2x-1=0.

En dålig lösning:


x^2 + 2x - 1 = 0

x = -2/2 ± sqrt[(2/2)^2-(-1)]

x = -1 ± sqrt(2)

Svar:

x1 = -1+sqrt(2)

x2 = -1-sqrt(2)

En bra lösning:


Jag använder pq-formeln för att lösa uppgiften. Insättning i pq-formeln ger

x = -2/2 ± sqrt[(2/2)^2-(-1)]

vilket förkortas till

x = -1 ± sqrt(2)

Alltså har ekvationen två rötter, x=-1+sqrt(2) samt x=-1-sqrt(2).

Vilken av ovanstående lösningar tycker du är lättare att hänga med?


Att kopiera över en definition från kompendiet och använda det som motivering är inte tillräckligt. Du måste också med egna ord förklara varför definitionen är uppfylld.

Exempel 2 (Definition som motivering)

Definition: Ett tal är rationellt om det kan skrivas på formen \displaystyle a/b där \displaystyle a och \displaystyle b\neq0 är heltal.

Uppgift: Är \displaystyle 3,05 ett rationellt tal?

Ett dåligt svar:


Ja, eftersom 3,05 kan skrivas på formen a/b där a och b är heltal.

Ett bra svar:


Ett tal är rationellt om det kan skrivas på formen a/b, där a och b är heltal. Vi kan skriva 3,05=a/b om vi väljer a=305 och b=100. Alltså är 3,05 rationellt.


När du kompletterar, markera tydligt var kompletteringen börjar. Alternativt kan du ta bort ditt tidigare svar och skriva en helt ny lösning. Det händer ofta att man skriver sin nya lösning direkt efter den gamla så att det blir svårt för mentorerna att bedöma om studenten verkligen har förstått.

Exempel 3 (Otydlig komplettering)

Uppgift: Hur många rötter har polynomet \displaystyle f(x)=x^2+1?

Lösning 1:


Vi har f(x)=x^2+1=0 vilket är ekvivalent med x^2=-1. Ett tal gånger sig själv kan aldrig vara negativt, alltså saknar polynomet rötter.

Rättning 1:


Kan det inte finnas komplexa rötter?

/mentorerna

---

Vi har f(x)=x^2+1=0 vilket är ekvivalent med x^2=-1. Ett tal gånger sig själv kan aldrig vara negativt, alltså saknar polynomet rötter.

Lösning 2:


Vi har f(x)=x^2+1=0 vilket är ekvivalent med x^2=-1. Ett tal gånger sig själv kan aldrig vara negativt, alltså saknar polynomet rötter. Ekvationen x^2=-1 har lösningarna x=+/-i, alltså har polynomet två rötter.

Rättning 2:


Du ger ju två olika svar på frågan!

/mentorerna

---

Vi har f(x)=x^2+1=0 vilket är ekvivalent med x^2=-1. Ett tal gånger sig själv kan aldrig vara negativt, alltså saknar polynomet rötter. Ekvationen x^2=-1 har lösningarna x=+/-i, alltså har polynomet två rötter.




Att vara systematisk

Vi rekommenderar att du läser igenom de avsnitt i kompendiet som inlämningsuppgiften behandlar. Att försöka lösa inlämningsuppgifterna utan att läsa teori funkar oftast inte. Innan du lämnar in något, läs genom din lösning. För att bli godkänd måste du ha svarat på alla delfrågor och motiverat dina svar. Kom ihåg att vara tydlig!

Här hittar du en lista över viktiga avsnitt:

  • Inlämningsuppgift 2: Avsnitt 2.1-2.2. Se även inspelningen av Lektion 3.
  • Inlämningsuppgift 3.1: Avsnitt 3.1-3.2. Se även inspelningen av Lektion 5 samt extra övningsuppgifter till avsnitt 3.2.
  • Inlämningsuppgift 3.2: Avsnitt 3.3-3.4. Se även inspelningen av Lektion 5 och 6.
  • Inlämningsuppgift 4.1: Avsnitt 4.1-4.2. Se även inspelningen av Lektion 7.
  • Inlämningsuppgift 4.2: Avsnitt 4.3. Se även inspelningen av Lektion 8.
  • Inlämningsuppgift 5: Specialiseringstexten (se Kurslitteratur)

Ni förväntas även känna till de tidigare avsnitten! För ett mer detaljerat dagsschema, se Studieplan.


Att lösa inlämningsuppgifter


Den här artikeln är hämtad från http://wiki.sommarmatte.se/wikis/forberedandematte/index.php/Att_skriva_l%C3%B6sningar