14. Minsta kvadratmetoden
SamverkanLinalgLIU
| Rad 1: | Rad 1: | ||
Läs textavsnitt [http://wiki.math.se/wikis/samverkan/linalg-LIU/img_auth.php/6/60/Kapitel14.pdf 14 Minsta kvadratmetoden]. | Läs textavsnitt [http://wiki.math.se/wikis/samverkan/linalg-LIU/img_auth.php/6/60/Kapitel14.pdf 14 Minsta kvadratmetoden]. | ||
| - | Du har nu läst om minsta kvadratmetoden och här kommer några övningar som testar om du har tagit till dig stoffet. | + | Du har nu läst om minsta kvadratmetoden och här kommer några övningar som testar om du har tagit till dig stoffet. {\color{Blue}filminspelning} |
Versionen från 21 oktober 2011 kl. 16.17
Läs textavsnitt 14 Minsta kvadratmetoden.
Du har nu läst om minsta kvadratmetoden och här kommer några övningar som testar om du har tagit till dig stoffet. {\color{Blue}filminspelning}
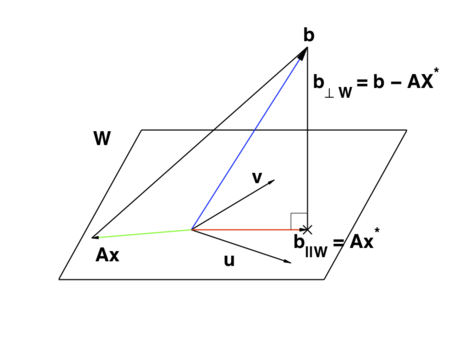
Klicka på bilden för att se en {\color{Blue}filminspelning} om minstakvadratmetoden.
Innehåll |
Övning 15.1
Ange den linje \displaystyle y=kx+m som i minsta kvadratmening bäst ansluter till punkterna \displaystyle (-1,-3) , \displaystyle (1,-2) och \displaystyle (3,5) . Rita figur!
Övning 15.2
a) Ange den linje, \displaystyle y=kx+m , som i minsta kvadratmening ansluter sig bäst till
\begin{matrix} \begin{matrix}
x &\vert& \phantom{-}2& \vert& 3& \vert& \phantom{-}4 &\vert& 5\\
\end{matrix}\\[-3pt] \rule 150pt 0.4pt 0pt\\ \begin{matrix}
y &\vert& -2& \vert& 0 & \vert & -1 & \vert & 1
\end{matrix} \end{matrix}
b) Beräkna också \displaystyle \sum_{j=1}^4(kx_j+m-y_j)^2 .
Övning 15.3
Ange den andragradskurva \displaystyle y=ax^2+bx+c , som i minsta kvadratmening bäst ansluter till följande mätdata
\begin{matrix} \begin{matrix}
x &\vert& -1& \vert& 0& \vert& 1 &\vert& 2\\
\end{matrix}\\[-3pt] \rule 150pt 0.4pt 0pt\\ \begin{matrix}
y &\vert& \phantom{-}2& \vert& 2 & \vert & 1 & \vert & 0
\end{matrix} \end{matrix}
Övning 15.4
Jämför med Exempel 12.29. Låt \displaystyle \boldsymbol{u}=(1,0,0)^t och
W=[(1,2,2)^t,(3,0,3)^t]\subset{\bf E}^3.
a) Bestäm med minsta kvadratmetoden (MK-metoden) den ortogonala projektionen \displaystyle \boldsymbol{u}_{\parallel W} .
b) Bestäm avståndet mellan punkten \displaystyle (1,0,0) och planet \displaystyle W .
Övning 15.5
Bestäm med MK-metoden den vektor i
W=[(1,-1,1,-1)^t,(2,0,2,0)^t]\subset{\bf E}^4.
som ligger närmast \displaystyle \boldsymbol{u}=(1,2,3,4)^t . (Jfr med Exempel 12.30.)
Övning 15.6
Låt
W=[(1,0,2,2)^t,(1,0,0,1)^t,(1,0,-1,5)^t]\subset{\bf E}^4
och \displaystyle \boldsymbol{u}=(2,3,6,2)^t . (Jfr med Exempel 12.33.)
a) Bestäm med MK-metoden den ortogonala projektionen \displaystyle \boldsymbol{u}_{\parallel W} .
b) Bestäm avståndet mellan punkten \displaystyle (2,3,6,2) och hyperplanet \displaystyle W .
Övning 15.7
Jämför med Exempel 12.34. Betrakta underrummet
W=\{\boldsymbol{x}\in{\bf E}^3:\ 2x_1-x_2-2x_3=0\}.
Låt \displaystyle \boldsymbol{u}=(x_1,x_2,x_3)^t\in{\bf E}^3 vara godtycklig.
a) Bestäm m.h.a. MK-metoden den ortogonala projektionen \displaystyle P_{W^\perp}(\boldsymbol{u}) .
b) Enligt Exempel 12.34 så är \displaystyle W=[(2,2,1)^t,(1,-2,2)]^t . Bestäm m.h.a. MK-metoden den ortogonala projektionen \displaystyle P_{W}(\boldsymbol{u}) .

 Hämtar...
Hämtar...